题目内容
二次函数 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出方程 的两个根;
的两个根;
(2)写出 随
随 的增大而减小的自变量
的增大而减小的自变量 的取值范围;
的取值范围;
(1)X=1或X=3;(2)X>2
解析考点:抛物线与x轴的交点;函数自变量的取值范围;二次函数的性质.
分析:(1)根据图象与x轴交点的坐标即可得到方程ax2+bx+c=0的两个根;
(2)由于抛物线是轴对称的图形,根据图象与x轴交点的坐标即可得到对称轴方程,由此再确定y随x的增大而减小的自变量x的取值范围.
解答:解:(1)根据图象得二次函数y=ax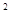 +bx+c(a≠0)的图象与x轴交点坐标为(1,0)、(3,0),
+bx+c(a≠0)的图象与x轴交点坐标为(1,0)、(3,0),
∴方程ax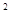 +bx+c=0的两个根为x
+bx+c=0的两个根为x =1,x
=1,x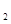 =3;
=3;
(2)根据图象得二次函数y=ax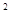 +bx+c(a≠0)的图象与x轴交点坐标为(1,0)、(3,0),
+bx+c(a≠0)的图象与x轴交点坐标为(1,0)、(3,0),
∴抛物线的对称轴为x=2,
∴当x≥2时,y随x的增大而减小.
点评:此题主要考查了二次函数与一元二次方程、一元二次不等式之间的联系:当y=0时,函数为一元二次方程;当y>0或y<0时,函数为一元二次不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
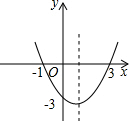 已知二次函数的图象如图所示,则这个二次函数的表达式为( )
已知二次函数的图象如图所示,则这个二次函数的表达式为( )| A、y=x2-2x+3 | B、y=x2-2x-3 | C、y=x2+2x-3 | D、y=x2+2x+3 |
 16、已知二次函数的图象如图所示,则
16、已知二次函数的图象如图所示,则 21、已知二次函数的图象如图所示,求它的解析式.
21、已知二次函数的图象如图所示,求它的解析式. 二次函数的图象如图所示,P为图象顶点,A为图象与y轴交点.
二次函数的图象如图所示,P为图象顶点,A为图象与y轴交点. 二次函数的图象如图所示,则a
二次函数的图象如图所示,则a