��Ŀ����
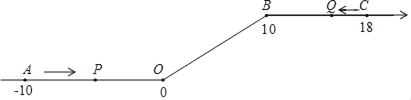
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ�����������ᡱ��ͼ�е�A��ʾ��10����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������28�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ����š��������ᡱ���������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룻��P�ӵ�A������ͬʱ����Q�ӵ�C��������1��λ/����ٶ����š��������ᡱ�ĸ������˶�������P����B��ʱ����P��Q��ֹͣ�˶������˶���ʱ��Ϊt�룮�ʣ�
��1���ú�t�Ĵ���ʽ��ʾ����P���˶������о�O��ľ��룻
��2��P��Q��������ʱ���������ʱ�估������M����Ӧ�����Ƕ��٣�
��3���Ƿ����P��O���������������ij�����Q��B���������������ij������ʱ�������ڣ���ֱ��д��t��ȡֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2������ʱ��Ϊ
����2������ʱ��Ϊ![]() �룬��M����Ӧ������
�룬��M����Ӧ������![]() ����3�����ڣ�t��2��t��
����3�����ڣ�t��2��t��![]() ��
��
��������
��1���ֵ�P��AO�Ϻ͵�P��OB������������������P��ÿ��ʱt��ȡֵ��Χ���ٸ�������ֱ��г�����ʽ�ɵô𰸣�
��2����������ʱP��Q�˶���ʱ����ȣ�P��Q�˶��ľ���͵���28�ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��3����0��t��5��5��t��8��8��t��15�������������PO=BQ���ɵ÷��̣��ֱ������̣��ɵô𰸣�
�⣺��1���趯��P���˶������о�O��ľ���ΪS����P��A�˶���Oʱ,����ʱ��Ϊ��![]() ���룩��
���룩��
��0��t��5ʱ��S��10��2t��
��P��O�˶���Bʱ,����ʱ��Ϊ��![]() ���룩
���룩
��P��A�˶���Bʱ,����ʱ��Ϊ��15��
��5��t��15ʱ��S��t��5��
������P���˶������о�O��ľ���S��![]() ��
��
��2���辭��a�룬P��Q�������������P�˶��ľ���Ϊ10+��a-5������Q�˶��ľ���Ϊa,
10+��a-5��+a=28
��ã�a��![]() ��
��
���M����Ӧ�����ǣ�18��![]() ��
��![]() ��
��
����M����Ӧ������![]() ��
��
��3�����ڣ�t��2��t��![]() ��
��
���ɣ���0��t��5ʱ��
10��2t����18��10��t����1��
��ã�t��2
��5��t��8ʱ��
��t��10��2����1����18��10��t����1��
��ã�t��![]() ��
��
��8��t��15ʱ��
��t��10��2����1��[t����18��10����1]��1
�÷����⣬
�ʴ��ڣ�t��2��t��![]() ��
��
�ʴ�Ϊ����1��![]() ����2������ʱ��Ϊ
����2������ʱ��Ϊ![]() �룬��M����Ӧ������
�룬��M����Ӧ������![]() ����3�����ڣ�t��2��t��
����3�����ڣ�t��2��t��![]() ��
��