̀âÄ¿ÄÚÈƯ
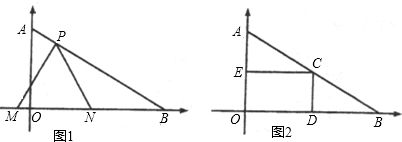
Èçͼ1£¬̉ÑÖªµăA£¨0£¬4
£©xÖáƠư°ëÖáÉÏ£¬Ç̉¡ÏABO=30¡ă£¬¶¯µăPÔÚÏ߶ÎABÉÏ´ÓµăAỊ̈µăB̉ÔĂ¿Ăë
¸öµ¥Î»µÄËÙ¶ÈÔ˶¯£¬ÉèÔ˶¯Ê±¼äΪtĂ룬ÔÚxÖáÉÏÈ¡Á½µăM¡¢N×÷µÈ±ß¡÷PMN£®

£¨1£©ÇóÖ±ÏßABµÄ½âÎöʽ£»
£¨2£©ÇóµÈ±ß¡÷PMNµÄ±ß³¤£¨ÓĂtµÄ´úÊưʽ±íʾ£©£¬²¢Çó³öµ±¶¥µăMÔ˶¯µ½ÓëÔµăOÖغÏʱtµÄÖµ£»
£¨3£©Èçͼ2£¬Èç¹ûÈ¡OBµÄÖеăD£¬̉ÔODΪ±ßÔÚRt¡÷AOBÄÚ²¿×÷¾ØĐÎODCE£¬µăCÔÚÏ߶ÎABÉÏ£¬´ÓµăP¿ªÊ¼Ô˶¯µ½µăMÓëÔµăOÖغÏƠẩ»¹ư³̀ÖĐ£¬ÉèµÈ±ß¡÷PMNºÍ¾ØĐÎODCEÖص₫²¿·ÖµÄĂæ»ưΪS£¬ÇëÇó³öSÓëtµÄº¯Êư¹ØϵʽºÍÏàÓ¦µÄ×Ô±äÁ¿tµÄÈ¡Öµ·¶Î§£®
| 3 |
| 3 |

£¨1£©ÇóÖ±ÏßABµÄ½âÎöʽ£»
£¨2£©ÇóµÈ±ß¡÷PMNµÄ±ß³¤£¨ÓĂtµÄ´úÊưʽ±íʾ£©£¬²¢Çó³öµ±¶¥µăMÔ˶¯µ½ÓëÔµăOÖغÏʱtµÄÖµ£»
£¨3£©Èçͼ2£¬Èç¹ûÈ¡OBµÄÖеăD£¬̉ÔODΪ±ßÔÚRt¡÷AOBÄÚ²¿×÷¾ØĐÎODCE£¬µăCÔÚÏ߶ÎABÉÏ£¬´ÓµăP¿ªÊ¼Ô˶¯µ½µăMÓëÔµăOÖغÏƠẩ»¹ư³̀ÖĐ£¬ÉèµÈ±ß¡÷PMNºÍ¾ØĐÎODCEÖص₫²¿·ÖµÄĂæ»ưΪS£¬ÇëÇó³öSÓëtµÄº¯Êư¹ØϵʽºÍÏàÓ¦µÄ×Ô±äÁ¿tµÄÈ¡Öµ·¶Î§£®
·ÖÎö£º£¨1£©̉ÑÖªµăAµÄ×ø±êÖªµÀOAµÄ³¤¶È£¬ÔÚÖ±½ÇÈư½ÇĐÎÖиù¾Ư30¡ăËù¶ÔµÄÖ±½Ç±ßµÈÓÚб±ßµÄ̉»°ëÇó³öAB£¬¸ù¾Ư¹´¹É¶¨ÀíÇó³öOB£¬´Ó¶øÇó³öBµÄ×ø±ê£¬×îºóÀûÓĂ´ư¶¨ÏµÊư·¨Çó³öÖ±ÏßABµÄ½âÎöʽ£®
£¨2£©ÓÉ£¨1£©̉ѾÇó³öABµÄ³¤£¬¿É̉Ô±íʾ³öBPµÄ³¤£¬̀âÄ¿̉²¸æËßÁË¡ÏABOµÄ¶ÈÊư£¬ÀûÓĂÈư½Çº¯ÊưÖµ¾Í¿É̉Ô±íʾ³öMP³¤¶È£¬µ±Mµ½´ïOµăÀûÓĂ30¡ăµÄÖ±½ÇÈư½ÇĐεÄ̀ØÊâ¹ØϵÇó³öOP£¬ÀûÓĂ¹´¹É¶¨Àí¾Í¿É̉ÔÇó³öAP£¬´Ó¶øÇó³öʱ¼ät£®
£¨3£©µ±µăMÓëÔµăOÖغÏʱ£¬µăNÓëµăD̉²ÊÇÖغϵģ¬Ơâʱ̉ÔPMÊÇ·ñ¹ưµăEΪ·Öµă·Ö±đ¼ÆËăÖغϲ¿·ÖµÄĂæ»ư£®½«Öغϲ¿·ÖµÄĂæ»ưÓĂº¬tµÄʽ×Ó±íʾ³öÀ´¾Í¿É̉ÔÁË£®
£¨2£©ÓÉ£¨1£©̉ѾÇó³öABµÄ³¤£¬¿É̉Ô±íʾ³öBPµÄ³¤£¬̀âÄ¿̉²¸æËßÁË¡ÏABOµÄ¶ÈÊư£¬ÀûÓĂÈư½Çº¯ÊưÖµ¾Í¿É̉Ô±íʾ³öMP³¤¶È£¬µ±Mµ½´ïOµăÀûÓĂ30¡ăµÄÖ±½ÇÈư½ÇĐεÄ̀ØÊâ¹ØϵÇó³öOP£¬ÀûÓĂ¹´¹É¶¨Àí¾Í¿É̉ÔÇó³öAP£¬´Ó¶øÇó³öʱ¼ät£®
£¨3£©µ±µăMÓëÔµăOÖغÏʱ£¬µăNÓëµăD̉²ÊÇÖغϵģ¬Ơâʱ̉ÔPMÊÇ·ñ¹ưµăEΪ·Öµă·Ö±đ¼ÆËăÖغϲ¿·ÖµÄĂæ»ư£®½«Öغϲ¿·ÖµÄĂæ»ưÓĂº¬tµÄʽ×Ó±íʾ³öÀ´¾Í¿É̉ÔÁË£®
½â´đ£º½â£º£¨1£©¡ßA£¨0£¬4
£©
¡àOA=4
£¬
ÔÚRt¡÷AOBÖĐ£¬¡ÏAOB=90¡ă£¬
¡àtan¡ÏABO=
£¬¼´tan30¡ă=
=
£¬
¡àBO=12£¬
¡àB£¨12£¬0£©
ÉèÖ±ÏßABµÄ½âÎöʽΪ£ºy=kx+b£¬ÓÉ̀ẩâµĂ£º
£¬
½âµĂ£º
£¬
¹ÊÖ±ÏßABµÄ½âÎöʽΪ£ºy=-
x+4
£»
£¨2£©¡ß¡÷PMNΪµÈ±ßÈư½ÇĐΣ¬
¡à¡ÏPMO=60¡ă£¬
¡ß¡ÏABO=30¡ă£¬
¡à¡ÏPMO+¡ÏABO=90¡ă£¬
¡à¡ÏMPB=90¡ă£¬
ÔÚRt¡÷AOBÖĐ£¬¡ÏAOB=90¡ă£¬¡ÏABO=30¡ă£¬
¡àAB=2AO=8
£¬
¡àBP=AB-AP=8
-
t£¬
ÔÚRt¡÷MPBÖĐ£¬¡ÏMPB=90¡ă£¬tan¡ÏABO=
£¬
¼´tan30¡ă=
=
£¬
¡àMP=8-t£¬
µ±MÓëOÖغÏʱ£¬ÔÚRt¡÷PBOÖĐ£¬¡ÏABO=30¡ă£¬¡ÏBPO=90¡ă£¬
¡àMP=
OB=6£¬¼´8-t=6£¬
¡àt=2£»
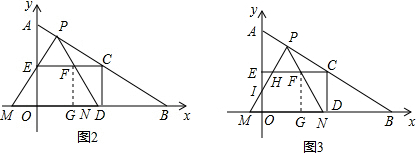
£¨3£©MÓëOµăÖغÏʱPM=MN=6£¬´ËʱNµăÓëDµăÖغϣ¬Èçͼ2£¬
µ±PM¹ưµăEʱ£¬¡ÏPMB=60¡ă£¬¡ÏMBA=30¡ă£¬
¡à¡ÏMBA=¡ÏACE=30¡ă£¬
¡à¡ÏEAP=60¡ă£¬
 ¡à¡ÏAEP=30¡ă£¬
¡à¡ÏAEP=30¡ă£¬
¡àAP=
AE=
£¬
´Ëʱt=1£»
µ±0¡Üt¡Ü1ʱ£¬ÉèPN½»ECÓÚF£¬¹ưF×÷FG¡ÍOBÓÚG£¬FG=OE=2
£¬
¡ß¡ÏPNM=60¡ă£¬
¡àGN=
=2£¬
¡ßPM=8-t£¬
¡àBM=2PM=16-2t£¬
¡àMO=BM-BO=4-2t£¬ON=MN-MO=t+4£¬EF=OG=ON-GN=t+2£¬
¡àS=
¡Á2
¡Á£¨t+2+t+4£©
=2
t+6
£¬
µ±0£¼t¡Ü2ʱ£¬ÉèPM¡¢PN½»ECÓÚH¡¢F£¬S=S̀ƯĐÎEONF-S¡÷EHI£®
ÓÉ£¨2£©Öª£ºMO=4-2t£¬IO=
MO=4
-2
t£¬
¡àEI=EO-IO=2
t-2
£¬EH=
EI=2t-2£¬
¡àS¡÷EHI=
¡Á£¨2t-2£©¡Á£¨2
t-2
£©=2
t2-4
t+2
£¬
¡àS=2
t+6
-2
t2+4
t-2
=-2
t2+6
t+4
£®
| 3 |
¡àOA=4
| 3 |
ÔÚRt¡÷AOBÖĐ£¬¡ÏAOB=90¡ă£¬
¡àtan¡ÏABO=
| OA |
| OB |
4
| ||
| OB |
| ||
| 3 |
¡àBO=12£¬
¡àB£¨12£¬0£©
ÉèÖ±ÏßABµÄ½âÎöʽΪ£ºy=kx+b£¬ÓÉ̀ẩâµĂ£º
|
½âµĂ£º
|
¹ÊÖ±ÏßABµÄ½âÎöʽΪ£ºy=-
| ||
| 3 |
| 3 |
£¨2£©¡ß¡÷PMNΪµÈ±ßÈư½ÇĐΣ¬
¡à¡ÏPMO=60¡ă£¬
¡ß¡ÏABO=30¡ă£¬
¡à¡ÏPMO+¡ÏABO=90¡ă£¬
¡à¡ÏMPB=90¡ă£¬
ÔÚRt¡÷AOBÖĐ£¬¡ÏAOB=90¡ă£¬¡ÏABO=30¡ă£¬
¡àAB=2AO=8
| 3 |
¡àBP=AB-AP=8
| 3 |
| 3 |
ÔÚRt¡÷MPBÖĐ£¬¡ÏMPB=90¡ă£¬tan¡ÏABO=
| MP |
| BP |
¼´tan30¡ă=
| MP | ||||
8
|
| ||
| 3 |
¡àMP=8-t£¬
µ±MÓëOÖغÏʱ£¬ÔÚRt¡÷PBOÖĐ£¬¡ÏABO=30¡ă£¬¡ÏBPO=90¡ă£¬
¡àMP=
| 1 |
| 2 |
¡àt=2£»
£¨3£©MÓëOµăÖغÏʱPM=MN=6£¬´ËʱNµăÓëDµăÖغϣ¬Èçͼ2£¬
µ±PM¹ưµăEʱ£¬¡ÏPMB=60¡ă£¬¡ÏMBA=30¡ă£¬
¡à¡ÏMBA=¡ÏACE=30¡ă£¬
¡à¡ÏEAP=60¡ă£¬
 ¡à¡ÏAEP=30¡ă£¬
¡à¡ÏAEP=30¡ă£¬¡àAP=
| 1 |
| 2 |
| 3 |
´Ëʱt=1£»
µ±0¡Üt¡Ü1ʱ£¬ÉèPN½»ECÓÚF£¬¹ưF×÷FG¡ÍOBÓÚG£¬FG=OE=2
| 3 |
¡ß¡ÏPNM=60¡ă£¬
¡àGN=
| FG |
| tan60¡ă |
¡ßPM=8-t£¬
¡àBM=2PM=16-2t£¬
¡àMO=BM-BO=4-2t£¬ON=MN-MO=t+4£¬EF=OG=ON-GN=t+2£¬
¡àS=
| 1 |
| 2 |
| 3 |
=2
| 3 |
| 3 |
µ±0£¼t¡Ü2ʱ£¬ÉèPM¡¢PN½»ECÓÚH¡¢F£¬S=S̀ƯĐÎEONF-S¡÷EHI£®
ÓÉ£¨2£©Öª£ºMO=4-2t£¬IO=
| 3 |
| 3 |
| 3 |
¡àEI=EO-IO=2
| 3 |
| 3 |
| ||
| 3 |
¡àS¡÷EHI=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
¡àS=2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
µăÆÀ£º±¾̀⿼²éÁË̉»´Îº¯ÊưµÄ×ÛºÏÊỒ⣬¿¼²éÁËÔËÓĂ´ư¶¨ÏµÊư·¨Çóº¯ÊưµÄ½âÎöʽ£¬¹´¹É¶¨ÀíµÄÔËÓĂ£¬Èư½Çº¯ÊưµÄÔËÓẲÔ¼°Í¼ĐεÄĂæ»ư¹«Ê½£¬ÊưѧÖеĶ¯µăÎỀ⣮´Ë̀âÄѶȽϴó£¬×¢̉âƠÆÎƠÊưĐνáºÏ˼Ïë¡¢·ÖÀà̀ÖÂÛ˼ÏëÓë·½³̀˼ÏëµÄÓ¦ÓĂ£®

Á·Ï°²áϵÁĐ´đ°¸
Ïà¹Ø̀âÄ¿