题目内容
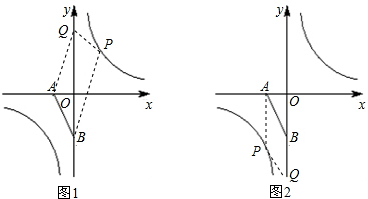
(2013•盐城模拟)如图1,已知点A(a,0),B(0,b),且a、b满足
+(a+b+3)2=0,?ABCD的边AD与y轴交于点E,且E为AD中点,双曲线y=
经过C、D两点.
(1)求k的值;
(2)点P在双曲线y=
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.

| a+1 |
| k |
| x |
(1)求k的值;
(2)点P在双曲线y=
| k |
| x |
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,
| MN |
| HT |

分析:(1)先根据非负数的性质求出a、b的值,故可得出A、B两点的坐标,设D(1,t),由DC∥AB,可知C(2,t-2),再根据平行四边形的性质求出t的值即可;
(2)由(1)知k=4可知反比例函数的解析式为y=
,再由点P在双曲线y=
上,点Q在y轴上,设Q(0,y),P(x,
),再分以AB为边和以AB为对角线两种情况求出x的值,故可得出P、Q的坐标;
(3)连NH、NT、NF,易证NF=NH=NT,故∠NTF=∠NFT=∠AHN,∠TNH=∠TAH=90°,MN=
HT由此即可得出结论.
(2)由(1)知k=4可知反比例函数的解析式为y=
| 4 |
| x |
| k |
| x |
| 4 |
| x |
(3)连NH、NT、NF,易证NF=NH=NT,故∠NTF=∠NFT=∠AHN,∠TNH=∠TAH=90°,MN=
| 1 |
| 2 |
解答:解:(1)∵
+(a+b+3)2=0,且
≥0,(a+b+3)2≥0,
∴
,
解得:
,
∴A(-1,0),B(0,-2),
∵E为AD中点,
∴xD=1,
设D(1,t),
又∵DC∥AB,
∴C(2,t-2),
∴t=2t-4,
∴t=4,
 ∴k=4;
∴k=4;
(2)∵由(1)知k=4,
∴反比例函数的解析式为y=
,
∵点P在双曲线y=
上,点Q在y轴上,
∴设Q(0,y),P(x,
),
①当AB为边时:
如图1所示:若ABPQ为平行四边形,则
=0,解得x=1,此时P1(1,4),Q1(0,6);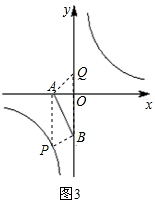
如图2所示;若ABQP为平行四边形,则
=
,解得x=-1,此时P2(-1,-4),Q2(0,-6);
②如图3所示;当AB为对角线时:AP=BQ,且AP∥BQ;
∴
=
,解得x=-1,
∴P3(-1,-4),Q3(0,2);
故P1(1,4),Q1(0,6);P2(-1,-4),Q2(0,-6);P3(-1,-4),Q3(0,2);
(3)连NH、NT、NF,
∵MN是线段HT的垂直平分线,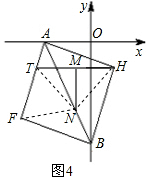
∴NT=NH,
∵四边形AFBH是正方形,
∴∠ABF=∠ABH,
在△BFN与△BHN中,
∵
,
∴△BFN≌△BHN,
∴NF=NH=NT,
∴∠NTF=∠NFT=∠AHN,
∴∠TNH=∠TAH=90°,
∴MN=
HT,
∴
=
.
| a+1 |
| a+1 |
∴
|
解得:
|
∴A(-1,0),B(0,-2),
∵E为AD中点,
∴xD=1,
设D(1,t),
又∵DC∥AB,
∴C(2,t-2),
∴t=2t-4,
∴t=4,
 ∴k=4;
∴k=4;(2)∵由(1)知k=4,
∴反比例函数的解析式为y=
| 4 |
| x |
∵点P在双曲线y=
| k |
| x |
∴设Q(0,y),P(x,
| 4 |
| x |
①当AB为边时:
如图1所示:若ABPQ为平行四边形,则
| -1+x |
| 2 |

如图2所示;若ABQP为平行四边形,则
| -1 |
| 2 |
| x |
| 2 |
②如图3所示;当AB为对角线时:AP=BQ,且AP∥BQ;
∴
| -1 |
| 2 |
| x |
| 2 |
∴P3(-1,-4),Q3(0,2);
故P1(1,4),Q1(0,6);P2(-1,-4),Q2(0,-6);P3(-1,-4),Q3(0,2);
(3)连NH、NT、NF,
∵MN是线段HT的垂直平分线,

∴NT=NH,
∵四边形AFBH是正方形,
∴∠ABF=∠ABH,
在△BFN与△BHN中,
∵
|
∴△BFN≌△BHN,
∴NF=NH=NT,
∴∠NTF=∠NFT=∠AHN,
∴∠TNH=∠TAH=90°,
∴MN=
| 1 |
| 2 |
∴
| MN |
| HT |
| 1 |
| 2 |
点评:本题考查的是反比例函数综合题,涉及到用待定系数法求反比例函数的解析式、正方形的性质、等腰三角形的判定与性质、全等三角形的判定与性质等相关知识,难度较大.

练习册系列答案
相关题目
 (2013•盐城模拟)如图所示,在建立平面直角坐标系后,△ABC顶点A的坐标为(1,-4),若以原点O为位似中心,在第二象限内画△ABC的位似图形△A′B′C′,使△A′B′C′与△ABC的位似比等于
(2013•盐城模拟)如图所示,在建立平面直角坐标系后,△ABC顶点A的坐标为(1,-4),若以原点O为位似中心,在第二象限内画△ABC的位似图形△A′B′C′,使△A′B′C′与△ABC的位似比等于
 (2013•盐城模拟)已知四边形ABCD的外接圆⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE•AC,BD=8,
(2013•盐城模拟)已知四边形ABCD的外接圆⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE•AC,BD=8,