题目内容
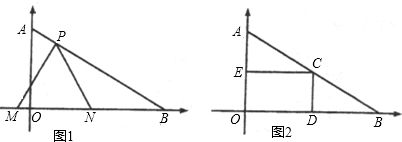
如图1,已知点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)请在图1中,找出与AD相等的线段,并说明理由;
(2)求∠DCA的大小;
(3)若点M在DE上,如图2,且DC=DM,求证:ME=BD.

(1)请在图1中,找出与AD相等的线段,并说明理由;
(2)求∠DCA的大小;
(3)若点M在DE上,如图2,且DC=DM,求证:ME=BD.

分析:(1)根据条件可以得出∠DAB=DBA,从而可以得出AD=BD;
(2)根据等腰直角三角形的性质可以得出△ADC≌△BDC,就可以得出∠DCA=∠DCB,从而可以得出结论;
(3)连结MC,证明△DCM是等边三角形,就可以得出CM=CD,∠MCE=45°,通过证明△MCE≌△DCB就可以得出结论.
(2)根据等腰直角三角形的性质可以得出△ADC≌△BDC,就可以得出∠DCA=∠DCB,从而可以得出结论;
(3)连结MC,证明△DCM是等边三角形,就可以得出CM=CD,∠MCE=45°,通过证明△MCE≌△DCB就可以得出结论.
解答:解:(1)BD=AD,
理由:∵△ABC是等腰直角三角形,
∴∠BAC=∠ABC=45°.
∵∠CAD=∠CBD=15°
∴∠BAC-∠CAD=∠ABC-∠CBD=45°-15°=30°,
即∠DAB=∠DBA,
∴BD=AD;
(2)∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∵在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
∴∠DCA=∠DCB,
∴∠DCA=
∠ACB=
×90°=45°;
 (3)连结MC,
(3)连结MC,
∵∠MDC=∠CAD+∠ACD,
∴∠MDC=15°+45°=60°.
∵DC=DM,
∴△DCM是等边三角形.
∴CD=CM=DM,∠CDM=∠DMC=∠DCM.
∵CE=CA,
∴∠CAE=∠CEA=15°,BC=CE,
∴∠ACE=150°
∴∠MCE=150°-45°-60°=45°,
∴∠MCE=∠DCB,
∵在△MCE和△DCB中,
,
∴△MCE≌△DCB(SAS),
∴ME=BD.
理由:∵△ABC是等腰直角三角形,
∴∠BAC=∠ABC=45°.
∵∠CAD=∠CBD=15°
∴∠BAC-∠CAD=∠ABC-∠CBD=45°-15°=30°,
即∠DAB=∠DBA,
∴BD=AD;
(2)∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∵在△ADC和△BDC中,
|
∴△ADC≌△BDC(SAS),
∴∠DCA=∠DCB,
∴∠DCA=
| 1 |
| 2 |
| 1 |
| 2 |
 (3)连结MC,
(3)连结MC,∵∠MDC=∠CAD+∠ACD,
∴∠MDC=15°+45°=60°.
∵DC=DM,
∴△DCM是等边三角形.
∴CD=CM=DM,∠CDM=∠DMC=∠DCM.
∵CE=CA,
∴∠CAE=∠CEA=15°,BC=CE,
∴∠ACE=150°
∴∠MCE=150°-45°-60°=45°,
∴∠MCE=∠DCB,
∵在△MCE和△DCB中,
|
∴△MCE≌△DCB(SAS),
∴ME=BD.
点评:本题考查了等腰直角三角形的性质的运用,等边三角形的判定与性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是解答本题的关键.

练习册系列答案
相关题目




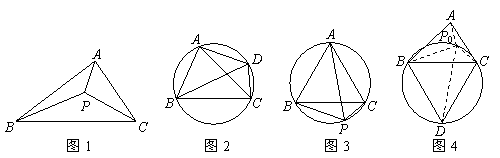 ②如图2,若四边形ABCD的四个顶点在同一个圆上,则有AB·CD+BC·AD=AC·BD.此为托勒密定理.
②如图2,若四边形ABCD的四个顶点在同一个圆上,则有AB·CD+BC·AD=AC·BD.此为托勒密定理.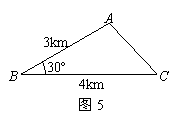 已知三村庄A、B、C构成了如图5所示的△ABC(其中∠A、∠B、∠C均小于120º),现选取一点P打水井,使水井P到三村庄A、B、C所铺设的输水管总长度最小.求输水管总长度的最小值.
已知三村庄A、B、C构成了如图5所示的△ABC(其中∠A、∠B、∠C均小于120º),现选取一点P打水井,使水井P到三村庄A、B、C所铺设的输水管总长度最小.求输水管总长度的最小值.