��Ŀ����
����Ŀ��ij�̳�ͳ����ÿ��ӪҵԱ��ij�µ����۶ͳ��ͼ���£�����ͳ��ͼ�и�������Ϣ������������⣺
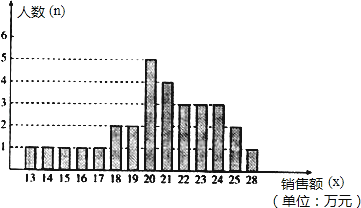
��1����ӪҵԱ�������۶�Ϊx����λ����Ԫ�����̳��涨����x��15ʱΪ����ְ����15��x��20ʱ��Ϊ������ְ����20��x��25Ϊ��ְ����x��25ʱΪ���㣮��ְ�������ӪҵԱ���ж����ˣ���ռ�ٷֱ��Ƕ��٣�
��2�����ݣ�1���й涨�����г�ְ���ϣ�ְ�ƺ����㣩��ӪҵԱ�����۶����λ����������ƽ�����ֱ��Ƕ��٣�
��3��Ϊ�˵���ӪҵԱ�Ĺ��������ԣ������ƶ������۶��������������������ӪҵԱ���ܵ����������Ҫʹ�ó�ְ���ϣ���ְ�����㣩��ӪҵԱ��һ���ܻ�����Ϊ���������Ӧ�������۶�Ϊ����Ԫ���ʣ������������ɣ�
���𰸡���1����������3�ˣ���ְ����18�ˣ���ռ�ٷֱ�Ϊ![]() ��100%=70%����2����λ����22��Ԫ��������20��Ԫ��ƽ������22
��100%=70%����2����λ����22��Ԫ��������20��Ԫ��ƽ������22![]() ����Ԫ������3�����������Ӧ�������۶�Ϊ22��Ԫ���ʣ�
����Ԫ������3�����������Ӧ�������۶�Ϊ22��Ԫ���ʣ�
��������
�����������1�����������ְ��������ӪҵԱ�������������ݰٷֱȵ�������⣻
��2��������λ����������ƽ�����������ɣ�
��3�����Ҫʹ�ó�ְ��������������ε�����ӪҵԱ�İ��������ܻ������۶�������Զ�Ϊ��ְ������������������۶����λ������Ϊ��λ�����ϵ�����ռ��������һ�����ң�
�⣺��1����ͼ��֪ӪҵԱ��������Ϊ2+1=3���ˣ���
��ͼ��֪ӪҵԱ������Ϊ1+1+1+1+1+2+2+5+4+3+3+3+2+1=30���ˣ���
���ְ����18�ˣ���ռ�ٷֱ�Ϊ![]() ��100%=70%��
��100%=70%��
��2����λ����22��Ԫ��
������20��Ԫ��
ƽ�����ǣ�![]() =22
=22![]() ����Ԫ����
����Ԫ����
��3�����������Ӧ�������۶�Ϊ22��Ԫ���ʣ�
��Ϊ��ְ���ϵ�ӪҵԱ�����۶����λ����22��Ԫ��˵�����۶�ﵽ�ͳ���22��Ԫ��ӪҵԱռ��ְӪҵԱ��һ�룬����ʹ��ְ����ӪҵԱ��һ���ܻ�