题目内容
【题目】如图,在△ABC 中,∠ABC=50°,∠ACB=80°,延长 CB 至 D,使 DB=BA,延长 BC 至 E,使 CE=CA,连接 AD 和 AE,求∠D,∠DAE 的度数.
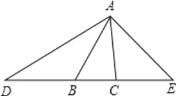
【答案】∠D=25°,∠DAE=115°.
【解析】
由DB=BA即可得到∠D=∠BAD,根据已知条件及三角形外角等于与它不相邻两个内角之和即可得到∠D的值,要求∠DAE,根据三角形内角和定理可知只需求出∠E即可.由CE=CA即可得到∠E=∠CAE,再结合三角形外角等于与它不相邻两个内角之和即可得到∠E的值,进而可得∠DAE的值.
解:∵∠ABC=50°,∠ACB=80°(已知),
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣50°﹣80°=50°(三角形内角和等于 180°),
∵DB=BA(已知),
∴∠D=∠DAB=![]() ∠ABC=25°(等边对等角),
∠ABC=25°(等边对等角),
∵CE=CA(已知),
∴∠E=∠CAE=![]() ∠ACB=40°(等边对等角),
∠ACB=40°(等边对等角),
∴∠DAE=∠DAB+∠BAC+∠CAE=25°+50°+40°=115°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目