��Ŀ����
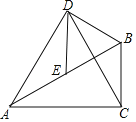
����Ŀ����ͼ1��������ƬABCD�ij�Ϊ2a����Ϊa�� Ϊ��Ҫ����Ƭ�ܴ���ֱ��Ϊ ![]() ��Բ�ף������Ƭ���д������涨��Ƭ��Բ���нӴ�ʱ��Ƭ���ܴ���Բ�ף���
��Բ�ף������Ƭ���д������涨��Ƭ��Բ���нӴ�ʱ��Ƭ���ܴ���Բ�ף��� 
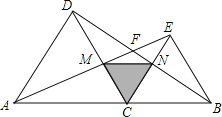
��1����ͼ2��M��N��P��Q�ֱ���AD��AB��BC��CD���е㣬����������Ƭ���ĸ���ȥ����ֻ�����ı���MNPQ�� �����ʱ��Ƭ��ʲô��״��
�ڸ���֤������ͨ������˵����ʱ��Ƭ���ܴ���Բ�ף�
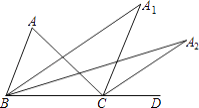
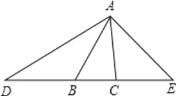
��2����ͼ3����������ƬABCD��������һ��ֱ�߷ֱ�BC��AD�ڵ�E��F������˵��غϣ�����������ֱ�߽�������Ƭ�и������ȫ�ȵ�ֱ��������Ƭ�� 
�ٵ�BE=DF= ![]() ʱ���ж�ֱ��������ƬEBAF�ܷ�Բ�ף���˵�����ɣ�
ʱ���ж�ֱ��������ƬEBAF�ܷ�Բ�ף���˵�����ɣ�
��Ϊ����ʹֱ��������ƬEBAF˳������Բ�ף���ֱ��д���߶�BE�ij��ȵ�ȡֵ��Χ��
���𰸡�
��1��������
����ͼ������M��MG��NP�ڵ�G��
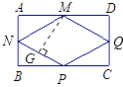
��M��N��P��Q�ֱ���AD��AB��BC��CD���е㣬
���AMN�ա�BPN�ա�CPQ�ա�DMQ��
��MN=NP=PQ=QM��
���ı���MNPQ�����Σ�
�� ![]() ��
��
MN= ![]() ��
��
��MG= ![]() ��
��
���ʱ��Ƭ�ܴ���Բ�ף�
��2������ͼ������A��AH��EF�ڵ�H������E��EK��AD�ڵ�K��
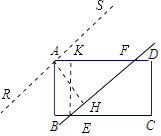
��ȻAB= ![]() ��
��
��������AB��ֱ�ķ���������Բ�ף�
����A��EF��ƽ����RS����ֻ�����ֱ��RS��EF֮��ľ��뼴�ɣ�
��BE=AK= ![]() ��EK=AB=a��AF=
��EK=AB=a��AF= ![]() ��
��
��KF= ![]() ��EF=
��EF= ![]() ��
��
�ߡ�AHF=��EKF=90�㣬��AFH=��EFK��
���AHF�ס�EKF��
�� ![]() ���ɵ�AH=
���ɵ�AH= ![]() ��
��
���ֱ��������Ƭ���ܴ���Բ�ף�
�� ![]() ��
�� ![]() ��
��
����������1��������������ȵ��ı���Ϊ�������ж��ı���Ϊ���Σ�Ȼ���������������������һ�ߵĸߣ�����֪���ݱȽϺ��ж��Ƿ���ͨ������2�����������������Ƶõ������߶Σ����������A��EF�ľ��룬Ȼ������֪�߶αȽϣ��Ӷ��ж��ܷ�ͨ����
�����㾫����������Ĺؼ���������ֱ����Բ������λ�ù�ϵ�����֪ʶ������ֱ����Բ������λ�ù�ϵ��������Ϊ���룻������������Ϊ�ཻ,����ֱ�߽���Բ�ĸ��ߣ�Բ��ֱ����Ψһ������Ϊ���У�����ֱ�߽���Բ�����ߣ����Ψһ�Ĺ���������е㣬�Լ������������ε��ж������ʵ����⣬�˽����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����