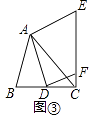题目内容
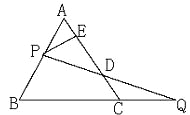
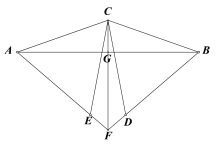
【题目】如图,△ABC为等腰三角形,AC=BC,△BDC和△ACE分别为等边三角形,直线AE与BD相交于点F,连接CF,交AB于点G.
(1)若∠ACB=150°,求∠AFB的度数;
(2)求证:AG=BG.
【答案】(1)90°;(2)详见解析.
【解析】
(1)由△BDC和△ACE分别为等边三角形可知∠CAF=∠CBD=60°,再由四边形的内角和为360°可求解∠AFB的度数;
(2)由AC=BC可得∠CAB=∠CBA,再由∠CAF=∠CBD=60°可得∠BAF=∠ABF,则AF=BF,据此易证△CAF≌△CBF得∠ACG=∠BCG,则可证明△ACG≌△BCG从而得到AG=BG.
(1)解:∵△BDC和△ACE分别为等边三角形,
∴∠CAF=∠CBD=60°,
∴∠AFB=360°-∠ACB-∠CAF-∠CBD=360°-150°-60°-60°=90°;
(2)证明:∵AC=BC,
∴∠CAB=∠CBA,
∵△BDC和△ACE分别为等边三角形,
∴∠CAF=∠CBD=60°,
∴∠BAF=∠CAF-∠CAB=∠CBD-∠CBA=∠ABF,
∴AF=BF,
∵AC=BC,∠CAF=∠CBD=60°,AF=BF,
∴△CAF≌△CBF,
∴∠ACG=∠BCG,
又∵AC=BC,∠CAB=∠CBA,
∴△ACG≌△BCG,
∴AG=BG.

练习册系列答案
相关题目