��Ŀ����
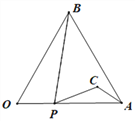
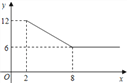
����Ŀ��ij��˾��Ӫ��÷ҵ����3��Ԫ/�ֵļ۸�������÷�ּ��A��B���࣬A����÷��װ��ֱ�����ۣ���װ�ɱ�Ϊ1��Ԫ/�֣�����ƽ�����ۼ۸�y����Ԫ/�֣�����������x��x��2����λ���֣�֮��ĺ�����ϵ��ͼ��B����÷��ӹ��������ۣ���ӹ��ܷ���s����Ԫ����ӹ�����t���֣�֮��ĺ�����ϵ��s=12+3t��ƽ�����ۼ۸�Ϊ9��Ԫ/�֣�
��1��A����÷��������Ϊ5��ʱ������ƽ�����ۼ۸���ÿ�ֶ�����Ԫ��
��2�����ù�˾�չ�10����÷������A����÷��4�֣���Ӫ������÷����õ�ë����w��Ϊ������Ԫ����ë����=���������멁��Ӫ�ܳɱ���
��3�����ù�˾�չ�20����÷��Ҫʹ�ù�˾���30��Ԫë������ֱ����A����÷�ж��ٶ֣�
���𰸡���1��9��Ԫ����2��30��Ԫ����3��18�֣�
�������������������1���ô���ϵ�������y��x�ĺ�������ʽ����x=5���뼴�ɣ�
��2�����ݡ�ë����=����������-��Ӫ�ܳɱ������㼴����ý��ۣ�
��3��������A����÷x�֣�������B����÷��20��x���֣��ֱ��ʾ��A��B���ֵ����̶���ʾ����������x��ȡֵ��Χ�ֱ���м��㼴�ɵ�.
�����������1����y=kx+b��k��0������x=2ʱ��y=12��x=8ʱ��y=6
�ã� ![]() �� ��ã�
�� ��ã� ![]() �� ��y=��x+14��2��x��8����
�� ��y=��x+14��2��x��8����
��x=5ʱ��y=9��
��A����÷��������Ϊ5��ʱ������ƽ�����ۼ۸���ÿ��9��Ԫ��
��2�����ù�˾�չ�10����÷������A����÷��4�֣���B����÷��6�֣�
�ã�WA=��10��3��1����4=24����Ԫ���� WB=6����9��3������12+3��6��=6����Ԫ����
��W=24+6=30����Ԫ����
�𣺴�ʱ��Ӫ������÷����õ�ë����wΪ30��Ԫ��
��3��������A����÷x�֣�������B����÷��20��x���֣�
��2��x��8ʱ�� wA=x����x+14����x=��x2+13x��
wB=9��20��x����[12+3��20��x��]=108��6x��
��w=wA+wB��3��20 =����x2+13x��+��108��6x����60 =��x2+7x+48��
��x��8ʱ��wA=6x��x=5x�� wB=9��20��x����[12+3��20��x��]=108��6x
��w=wA+wB��3��20=��5x��+��108��6x����60=��x+48��
��2��x��8ʱ����x2+7x+48=30�����x1=9��x2=��2�����������⣬
��x��8ʱ����x+48=30�����x=18��
�൱ë����ﵽ30��Ԫʱ��ֱ�����۵�A����÷��18�֣�