题目内容
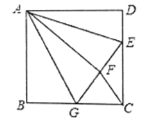
【题目】如图，在△ABC中，AE是∠BAC的角平分线，交BC于点E，DE∥AB交AC于点D．
(1)求证AD=ED；
(2)若AC=AB，DE=3，求AC的长．
【答案】(1)证明见解析；(2)6.
【解析】
（1）由AE是∠BAC的角平分线可得∠DAE=∠BAE，由DE∥AB，可得∠DEA=∠EAB，则∠DEA=∠DAE，可得结论．
（2）根据等腰三角形三线合一可得AE⊥BC，可证∠C=∠CED则CD=DE，即可求AC的长．
证明：(1)∵AE是∠BAC的角平分线
∴∠DAE=∠BAE，
∵DE∥AB
∴∠DEA=∠EAB，
∴∠DAE=∠DEA，
∴AD=DE-；
(2)∵AB=AC，AE是∠BAC的角平分线
∴AE⊥BC
∴∠C+∠CAE=90°，∠CED+∠DEA=90°，
∵∠CAE=∠DEA，
∴∠C=∠CED-
∴DE=CD
∴AD=DE=CD=3
∴AC=6.
故答案为：(1)证明见解析；(2)6.
练习册系列答案
53天天练系列答案
相关题目
【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表：
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分，求x和y的值；
(2)在(1)的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求a，b的值．
