题目内容
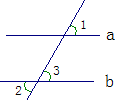25、完成推理填空：如图，已知∠1=∠2，说明：a∥b．证明：∵∠1=∠2 （已知）
∠2=∠3 （
对顶角相等
）∴∠1=∠3 （
等量代换
）∴a∥b （
同位角相等，两直线平行
）分析：通过已知图形得，∠1和∠3是同位角，根据已知∠1=∠2，又∠2和∠3是对顶角可证明∠1=∠3，同位角相等两直线平行．
解答：解：∵∠1=∠2（已知）
∠2=∠3（对顶角相等）
∴∠1=∠3（等量代换）
∴a∥b（同位角相等，两直线平行）．
故答案为：对顶角相等，等量代换，同位角相等，两直线平行．
∠2=∠3（对顶角相等）
∴∠1=∠3（等量代换）
∴a∥b（同位角相等，两直线平行）．
故答案为：对顶角相等，等量代换，同位角相等，两直线平行．
点评：此题考查了学生对平行线的判定的掌握，解答此题的关键是要明确通过同位角相等证明两直线平行．
练习册系列答案
阅读快车系列答案
相关题目
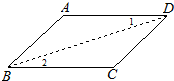24、完成推理填空：如图所示，已知AD=BC，AB=DC，试判断∠A与∠ABC的关系．下面是小颖同学的推导过程：
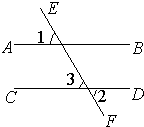25、完成推理填空：如图：直线AB、CD被EF所截，若已知AB∥CD，
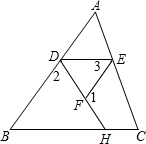完成推理填空：如图在△ABC中，已知∠1+∠2=180°，∠3=∠B，试说明∠AED=∠C．
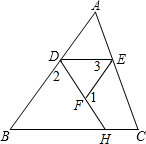完成推理填空：如图在△ABC中，已知∠1+∠2=180°，∠3=∠B，试说明∠AED=∠C．