题目内容
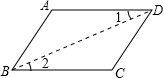
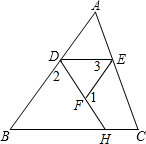 完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴________ ( 同角的补角相等 )
∴________ (内错角相等,两直线平行)
∴∠ADE=∠3________
∵∠3=∠B________
∴∠ADE=∠B(等量代换)
∴DE∥BC________
∴∠AED=∠C________.
∠EFD=∠2 AB∥EF (两直线平行,内错角相等) (已知) (同位角相等,两直线平行) (两直线平行,同位角相等)
分析:首先根据∠1+∠EFD=180°和∠1+∠2=180°可以证明∠EFD=∠2,再根据内错角相等,两直线平行可得AB∥EF,进而得到∠ADE=∠3,再结合条件∠3=∠B可得∠ADE=∠B,进而得到DE∥BC,再由平行线的性质可得∠AED=∠C.
解答:∵∠1+∠EFD=180°(邻补角定义),
又∵∠1+∠2=180°(已知),
∴∠EFD=∠2(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行),
∴∠ADE=∠3(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠ADE=∠B(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
点评:此题主要考查了平行线的判定与性质,关键是掌握平行线的判定定理和性质定理.
分析:首先根据∠1+∠EFD=180°和∠1+∠2=180°可以证明∠EFD=∠2,再根据内错角相等,两直线平行可得AB∥EF,进而得到∠ADE=∠3,再结合条件∠3=∠B可得∠ADE=∠B,进而得到DE∥BC,再由平行线的性质可得∠AED=∠C.
解答:∵∠1+∠EFD=180°(邻补角定义),
又∵∠1+∠2=180°(已知),
∴∠EFD=∠2(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行),
∴∠ADE=∠3(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠ADE=∠B(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
点评:此题主要考查了平行线的判定与性质,关键是掌握平行线的判定定理和性质定理.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
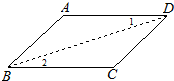 24、完成推理填空:如图所示,已知AD=BC,AB=DC,试判断∠A与∠ABC的关系.下面是小颖同学的推导过程:
24、完成推理填空:如图所示,已知AD=BC,AB=DC,试判断∠A与∠ABC的关系.下面是小颖同学的推导过程: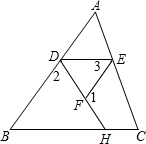 完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.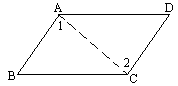
 解:连接BD.在△ABD与△CDB中
解:连接BD.在△ABD与△CDB中