ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥Τσ“ΒΫ”ΒΫ“Μ≈ζ≤ζΤΖΒΡ…ζ≤ζ»ΈΈώΘ§Α¥“Σ«σ±Ί–κ‘Ύ15ΧλΡΎΆξ≥…Θ°“―÷ΣΟΩΦΰ≤ζΤΖΒΡ έΦέΈΣ65‘ΣΘ§ΙΛ»ΥΦΉΒΎxΧλ…ζ≤ζΒΡ≤ζΤΖ ΐΝΩΈΣyΦΰΘ§y”κx¬ζΉψ»γœ¬ΙΊœΒΘΚ
y=![]() .
.
Θ®1Θ©ΙΛ»ΥΦΉΒΎΦΗΧλ…ζ≤ζΒΡ≤ζΤΖ ΐΝΩΈΣ80ΦΰΘΩ
Θ®2Θ©…ηΒΎxΧλΘ®0ΓήxΓή15Θ©…ζ≤ζΒΡ≤ζΤΖ≥…±ΨΈΣP‘Σ/ΦΰΘ§P”κxΒΡΚ· ΐΆΦœσ»γΆΦΘ§ΙΛ»ΥΦΉΒΎxΧλ¥¥‘λΒΡάϊ»σΈΣW‘ΣΘ°
ΔΌ«σP”κxΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΔΎ«σW”κxΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωΒΎΦΗΧλ ±Θ§άϊ»σΉν¥σΘ§Ήν¥σάϊ»σ «Εύ…ΌΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©ΒΎ14ΧλΘΜΘ®2Θ©ΔΌPΘΫ![]() ΘΜΔΎWΘΫ
ΘΜΔΎWΘΫ![]() ΘΜΒΎ14Χλ ±Θ§άϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ1280‘ΣΘ°
ΘΜΒΎ14Χλ ±Θ§άϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ1280‘ΣΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίyΘΫ80«σΒΟxΦ¥Ω…ΘΜ
Θ®2Θ©œ»ΗυΨίΚ· ΐΆΦœσ«σΒΟPΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘ§‘ΌΫαΚœxΒΡΖΕΈßΖ÷άύΧ÷¬έΘ§ΗυΨίΓΑΉήάϊ»σΘΫΒΞΦΰάϊ»σΓΝœζ έΝΩΓ±Ν–≥ωΚ· ΐΫβΈω ΫΘ§”…Εΰ¥ΈΚ· ΐΒΡ–‘÷ «σΒΟΉν÷ΒΦ¥Ω…Θ°
Θ®1Θ©ΗυΨίΧβ“βΘ§ΒΟΘΚΓΏ»τ8xΘΫ80Θ§ΒΟΘΚxΘΫ10ΘΨ5Θ§≤ΜΖϊΚœΧβ“βΘΜ
»τ5x+10ΘΫ80Θ§ΫβΒΟΘΚxΘΫ14Θ°
¥πΘΚΙΛ»ΥΦΉΒΎ14Χλ…ζ≤ζΒΡ≤ζΤΖ ΐΝΩΈΣ80ΦΰΘΜ
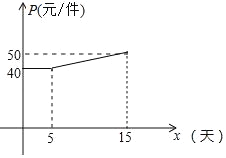
Θ®2Θ©ΔΌ”…ΆΦœσ÷ΣΘΚΒ±0ΓήxΓή5 ±Θ§PΘΫ40ΘΜ
Β±5ΘΦxΓή15 ±Θ§…ηPΘΫkx+bΘ§ΫΪΘ®5Θ§40Θ©Θ§Θ®15Θ§50Θ©¥ζ»κΒΟΘΚ![]() Θ§Γύ
Θ§Γύ![]() Θ§ΓύPΘΫx+35Θ°
Θ§ΓύPΘΫx+35Θ°
Ήέ…œΘ§P”κxΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚP![]() ΘΜ
ΘΜ
ΔΎΒ±0ΓήxΓή5 ±Θ§WΘΫΘ®65©¹40Θ©ΓΝ8xΘΫ200xΘ§Β±5ΘΦxΓή15 ±Θ§WΘΫΘ®65©¹x©¹35Θ©Θ®5x+10Θ©ΘΫ©¹5x2+140x+300Θ°
Ήέ…œΥυ ωΘΚW”κxΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚW![]() ΘΜ
ΘΜ
Β±0ΓήxΓή5 ±Θ§WΘΫ200xΘ°
ΓΏ200ΘΨ0Θ§ΓύWΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§ΓύΒ±xΘΫ5 ±Θ§WΉν¥σΈΣ1000‘ΣΘΜ
Β±5ΘΦxΓή15 ±Θ§WΘΫ©¹5Θ®x©¹14Θ©2+1280Θ§Β±xΘΫ14 ±Θ§WΉν¥σ÷ΒΈΣ1280‘ΣΘ°
Ήέ…œΥυ ωΘΚΒΎ14Χλ ±Θ§άϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ1280‘ΣΘ°