��Ŀ����
����Ŀ����֪����ƽ��ֱ������ϵ�У���P��0��2������PΪԲ�ģ�OPΪ�뾶�İ�Բ��y�����һ��������C��һ�κ���y=��![]() x+m��mΪʵ������ͼ��Ϊֱ��l��l�ֱ�x�ᣬy����A��B���㣬��ͼ1��
x+m��mΪʵ������ͼ��Ϊֱ��l��l�ֱ�x�ᣬy����A��B���㣬��ͼ1��
��1��B�������� ���ú�m�Ĵ���ʽ��ʾ������ABO= �㣻
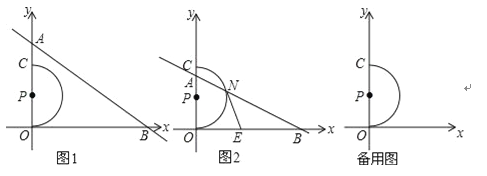
��2������N��ֱ��AB���ԲCO��һ�������㣨����������ʱ��NΪ�Ҳ�һ�㣩������N����P�����߽�x���ڵ�E����ͼ2��
���Ƿ����������m��ֵ��ʹ�á�EBN��ֱ�������Σ������ڣ����m��ֵ���������ڣ���˵�����ɣ�
�ڵ�![]() ʱ����m��ֵ��
ʱ����m��ֵ��
���𰸡���1��![]() ��30����2��m=2��3����3��m=
��30����2��m=2��3����3��m=![]() ��
��
��������
�����������1���������ֱ����x�ύ�����꣬�����ó��𰸣�������������Ǻ�����ϵ�ó���ABO�Ķ�����
��2���ٷֱ����á�NEB=90��͡�ENB=90�㣬������ߵ����ʵó�m��ֵ��
���������NG��EN=![]() ���ٵó���PHN�ס�NGE�����������������ε����ʣ������ó�m��ֵ��
���ٵó���PHN�ס�NGE�����������������ε����ʣ������ó�m��ֵ��
�����������1����y=0����0=��![]() x+m��
x+m��
��ã�x=![]() m��
m��
��B��������![]() ���ú�m�Ĵ���ʽ��ʾ����
���ú�m�Ĵ���ʽ��ʾ����
��һ�κ���y=��![]() x+m��y�ύ�ڵ㣨0��m����
x+m��y�ύ�ڵ㣨0��m����
��tan��ABO=![]() =
=![]() ��
��
���ABO=30�㣻
�ʴ�Ϊ��![]() ��30��
��30��
��2������ͼ�٣��������������m��ֵ��ʹ�á�EBN��ֱ�������Σ�����NP
����NEB=90�㣬��NE�ǡ�P�����ߣ�
���PNE=90�㣬
�ߡ�POE=90�㣬
���ı���OPNE�Ǿ��Σ�
��PN=2����APN=90�㣬
��Rt��APN�У�PN=2����BAO=60�㣬
��PA=1��
��m=3��
����ENB=90�㣬��NE�ǡ�P�����ߣ�
���PNE=90�㣬
���P��N��B���㹲�ߣ�����P���A�غϣ�
��m=2��
���Ͽ�֪��m=2��3��
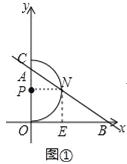
����ͼ�ڣ�����PN������E����EG��AB��G������P����PH��AB��H��
��PA=m��2��PH=![]() ��
��
��![]() ����EB=
����EB=![]() ��EN=EO=
��EN=EO=![]() ��EG=
��EG=![]() ��
��
��EG��EN=1��4����NG��EN=![]() ��
��
�ߡ�PNE=90�㣬���PNH+��ENG=90�㣬
�ߡ�GNE+��NEG=90�㣬
���NEG=��PNH��
�ߡ�PHN=��EGN=90�㣬
���PHN�ס�NGE��
��![]() ��
��
�� ��
��
��ã�m=![]() ��
��

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�