题目内容
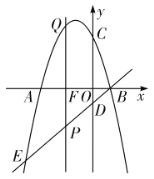
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,它与
,它与![]() 轴、
轴、![]() 轴的交点分别为
轴的交点分别为![]() 两点.
两点.

(1)若![]() 的半径为2,说明直线
的半径为2,说明直线![]() 与
与![]() 的位置关系;
的位置关系;
(2)若![]() 的半径为2,
的半径为2,![]() 经过点
经过点![]() 且与
且与![]() 轴相切于点
轴相切于点![]() ,求圆心
,求圆心![]() 的坐标;
的坐标;
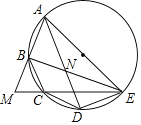
(3)若![]() 的内切圆圆心是点
的内切圆圆心是点![]() ,外接圆圆心是点
,外接圆圆心是点![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
【答案】(1)直线AB与⊙O的位置关系是相离;(2)(![]() ,2)或(-
,2)或(-![]() ,2);(3)
,2);(3)![]()
【解析】
(1)由直线解析式求出A(-4,0),B(0,3),得出OB=3,OA=4,由勾股定理得出AB=![]() =5,过点O作OC⊥AB于C,由三角函数定义求出OC=
=5,过点O作OC⊥AB于C,由三角函数定义求出OC=![]() >2,即可得出结论;
>2,即可得出结论;
(2)分两种情况:①当点P在第一象限,连接PB、PF,作PC⊥OB于C,则四边形OCPF是矩形,得出OC=PF=BP=2,BC=OB-OC=1,由勾股定理得出PC=![]() ,即可得出答案;②当点P在的第二象限,根据对称性可得出此时点P的坐标;
,即可得出答案;②当点P在的第二象限,根据对称性可得出此时点P的坐标;
(3)设⊙M分别与OA、OB、AB相切于C、D、E,连接MC、MD、ME、BM,则四边形OCMD是正方形,DE⊥AB,BE=BD,得出MC=MD=ME=OD=![]() (OA+OB-AB)=1,求出BE=BD=OB-OD=2,由直角三角形的性质得出△ABO外接圆圆心N在AB上,得出AN=BN=
(OA+OB-AB)=1,求出BE=BD=OB-OD=2,由直角三角形的性质得出△ABO外接圆圆心N在AB上,得出AN=BN=![]() AB=
AB=![]() ,NE=BN-BE=
,NE=BN-BE=![]() ,在Rt△MEN中,由勾股定理即可得出答案.
,在Rt△MEN中,由勾股定理即可得出答案.
解:(1)∵直线l的函数表达式为y=![]() x+3,
x+3,
∴当x=0时,y=3;当y=0时,x=4;
∴A(﹣4,0),B(0,3),
∴OB=3,OA=4,
AB=![]() =5,
=5,
过点O作OC⊥AB于C,如图1所示:
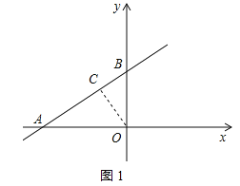
∵sin∠BAO=![]() ,
,
∴![]() ,
,
∴OC=![]() >2,
>2,
∴直线AB与⊙O的位置关系是相离;
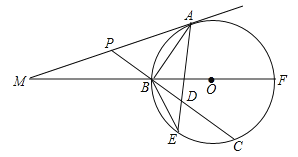
(2)如图2所示,分两种情况:
①当点P在第一象限时,连接PB、PF,作PC⊥OB于C,
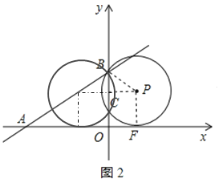
则四边形OCPF是矩形,
∴OC=PF=BP=2,
∴BC=OB﹣OC=3﹣2=1,
∴PC=![]() ,
,
∴圆心P的坐标为:(![]() ,2);
,2);
②当点P在第二象限时,
由对称性可知,在第二象限圆心P的坐标为:(-![]() ,2).
,2).
综上所知,圆心P的坐标为(![]() ,2)或(-
,2)或(-![]() ,2).
,2).
(3)设⊙M分别与OA、OB、AB相切于C、D、E,连接MC、MD、ME、BM,如图3所示:
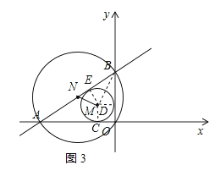
则四边形OCMD是正方形,DE⊥AB,BE=BD,
∴MC=MD=ME=OD=![]() (OA+OB﹣AB)=
(OA+OB﹣AB)=![]() ×(4+3﹣5)=1,
×(4+3﹣5)=1,
∴BE=BD=OB﹣OD=3﹣1=2,
∵∠AOB=90°,∴△ABO外接圆圆心N在AB上,
∴AN=BN=![]() AB=
AB=![]() ,∴NE=BN﹣BE=
,∴NE=BN﹣BE=![]() ﹣2=
﹣2=![]() ,
,
在Rt△MEN中,
MN=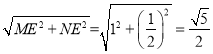 .
.