题目内容
【题目】如图,分别以△ABC的边AB,AC向外作等边△ABD和等边△ACE,线段BE与CD相交于点O,连接OA.
(1)请你完成图形(尺规作图,不写作法,保留作图痕迹);

(2)求证:BE=DC;
(3)求证:OA平分∠DOE.
【答案】(1)图形见解析(2)证明见解析(3)证明见解析
【解析】试题分析:(1)先分别以点A、B为圆心,以AB为半径画弧,交于点D,连接AD、BC;再分别以点A、C为圆心,以AC为半径画弧,交于点E,连接AE、CE即可.
(2)根据等边三角形性质得出AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,求出∠BAE=∠DAC.根据SAS证△ABE≌△ADC即可.
(3)过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.根据三角形的面积公式求出AN=AM,根据角平分线性质求出即可.
试题解析:(1)完成图形,如图所示:
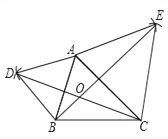
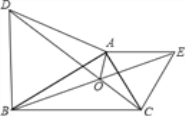
(2)证明:∵△ABD和△ACE都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,
∴∠BAC+∠CAE=∠BAC+∠BAD,
即∠BAE=∠DAC,
在△ABE和△ADC中,
∵AB=AD,∠BAE=∠DAC,AE=AC,
∴△ABE≌△ADC(SAS),
∴BE=DC.
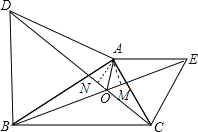
(3)证明:过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.
∵由(1)知:△ABE≌△ADC,
∴BE=DC,S△ABE=S△ADC,
∴![]() BEAM=
BEAM=![]() DCAN,
DCAN,
∴AM=AN,
∵AM⊥BE,AN⊥DC,
∴点A在∠DOE的平分线上,
即OA平分∠DOE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目