题目内容
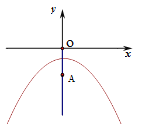
【题目】已知抛物线
（1）填空：抛物线的顶点坐标是（ ， ），对称轴是 ；
（2）已知y轴上一点A（0，-2），点P在抛物线上，过点P作PB⊥x轴，垂足为B．若△PAB是等边三角形，求点P的坐标；
（3）在（2）的条件下，点M在直线AP上．在平面内是否存在点 N，使以点O、点A、点M、点N为顶点的四边形为菱形？若存在，直接写出所有满足条件的点N的坐标；若不存在，请说明理由．
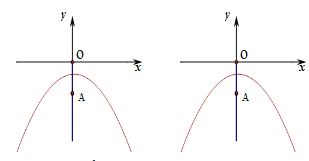
【答案】(1)、顶点(0，－1)，对称轴：y轴；(2)、P1（
） P2（
）；(3)、当点P的坐标为（） 时：N1（
） N2（－
），N3（
）；当点P的坐标为（）时，N4(
)， N5(
) , N6（
）
【解析】
试题分析：(1)、根据解析式可求得顶点坐标和对称轴；(2)、根据等边三角形的性质来进行求解，本题可以首先设出点P的坐标，然后求出PA、PB、AB的长度，然后根据等边三角形的性质进行计算；(3)、分两种情况根据菱形的性质求出点N的坐标.
试题解析：(1)、顶点（0，－1）， 对称轴： y轴（或直线 x = 0）
(2)、P1（） P2（）
(3)、当点P的坐标为（） 时：N1（） N2（－），N3（）；当点P的坐标为（）时，N4()， N5() , N6（）.
练习册系列答案
相关题目
