题目内容
在平面直角坐标系xOy中,有三条平行的直线l1,l2,l3,函数解析式依次为y=x,y=x+1,y=x+3,在这三条直线上各有一个动点,依次为A,B,C,它们的横坐标分别表示为a,b,c.则当a,b,c满足条件 ______ 时,这三点不能构成三角形.

分析:若不能构成三角形,就是这三个动点在一条直线上的时候,在一条直线有三种情况,(1)动点的横坐标相等;(2)动点的纵坐标相等;(3)三点满足一次函数式.
解答:解:(1)动点的横坐标相等时:a=b=c.
(2)动点的纵坐标相等时:∵y=a,y=b+1,y=c+3,∴a=b+1=c+3.
(3)三点满足一次函数式,三点可以表示一次函数的斜率:∵三点的坐标为(a,a),(b,b+1),(c,c+3),
∴ ,
,
1+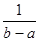 =1+
=1+ ,
,
∴ =3.
=3.
故答案为:a=b=c或a=b+1=c+3或 =3.
=3.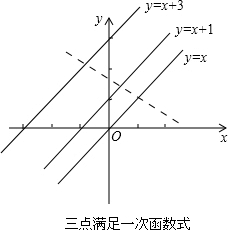
点评:本题考查两条直线相交或平行问题,关键是知道动点满足什么条件时不能构成三角形,即动点在同一直线上时不能三角形,从而可求解.
解答:解:(1)动点的横坐标相等时:a=b=c.

(2)动点的纵坐标相等时:∵y=a,y=b+1,y=c+3,∴a=b+1=c+3.

(3)三点满足一次函数式,三点可以表示一次函数的斜率:∵三点的坐标为(a,a),(b,b+1),(c,c+3),
∴
 ,
,1+
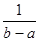 =1+
=1+ ,
,∴
 =3.
=3.故答案为:a=b=c或a=b+1=c+3或
 =3.
=3.
点评:本题考查两条直线相交或平行问题,关键是知道动点满足什么条件时不能构成三角形,即动点在同一直线上时不能三角形,从而可求解.

练习册系列答案
相关题目


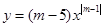 是正比例函数。
是正比例函数。
 .
. 500元,所获利润不少于2920元,不考虑其他因素,那么销售方案有哪几种?
500元,所获利润不少于2920元,不考虑其他因素,那么销售方案有哪几种? 率最大,请直接写出A、B两种品牌的服装各销售多少件?
率最大,请直接写出A、B两种品牌的服装各销售多少件?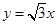 ,点
,点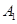 坐标为(1,0),过点
坐标为(1,0),过点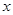 轴的垂线交直线于点
轴的垂线交直线于点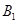 ,以原点
,以原点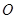 为圆心,
为圆心,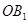 长为半径画弧交
长为半径画弧交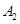 ;再过点
;再过点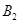 ,以原点
,以原点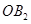 长为半径画弧交
长为半径画弧交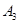 ,…,按此做法进行下去,点A1011的坐标为
,…,按此做法进行下去,点A1011的坐标为