题目内容
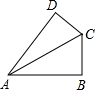如图四边形ABCD中，∠A=60°，∠B=∠D=90°，CD=2，BC=11，求AC的长．
分析：延长AD，BC交于点E，可得直角三角形ABE，易得CE长，利用30°的正切值可得AB的长，进而利用勾股定理可得AC长．
解答：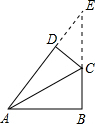
解：延长AD，BC交于点E，
∵∠A=60°，∠B=∠D=90°，
∴∠E=30°，
∵CD=2，
∴CE=2CD=4，
∴AB=BE×tan30°=
，
∴AC=
=14．
解：延长AD，BC交于点E，∵∠A=60°，∠B=∠D=90°，
∴∠E=30°，
∵CD=2，
∴CE=2CD=4，
∴AB=BE×tan30°=
15
| ||
| 3 |
∴AC=
| AB2+BC2 |
点评：考查解直角三角形的知识；作辅助线构造出特殊的直角三角形是解决本题的难点．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
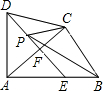如图四边形ABCD中，AD=DC．∠DAB=∠ACB=90°，过点D作DF⊥AC，垂足为F．DF与AB相交于E．设AB=15，BC=9，P是射线DF上的动点．当△BCP的周长最小时，DP的长为（ ）
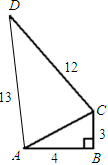已知，如图四边形ABCD中，∠B=90°，AB=4，BC=3，AD=13，CD=12，
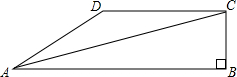如图四边形ABCD中，AC平分∠BAD，CD∥AB，BC=6cm，∠BAD=30°，∠B=90°．则CD的长为
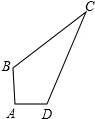已知，如图四边形ABCD中，∠A=90°，AB=4，AD=3，CD=13，BC=12，求：四边形ABCD的面积．