Question

【题目】直线l1交x轴于点A（6，0），交y轴于B（0，6）．

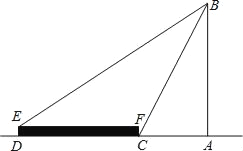
（1）如图，折叠△AOB，使BA落在y轴上，折痕所在直线为l2，直线l2与x轴交与C点，求C点坐标及l2的解析式；

（2）在直线l1上找点M，使得以M、A、C为顶点的三角形是等腰三角形，求出所有满足条件的M点的坐标．

Answer 1

【答案】（1）C（2，0），y＝﹣x+6；（2）点M（6﹣6，2）或（6+6，﹣2）或（4，2）或（0，6）．

【解析】

（1）由三角函数可求∠OAB＝30°，由折叠的性质和直角三角形的性质可求点C坐标，用待定系数法可求解析式；

（2）分三种情况讨论，由等腰三角形的性质可求解．

解：∵点A（6，0），交y轴于B（0，6）．

∴OA＝6，OB＝6，

∴tan∠OAB＝，

∴∠OAB＝30°，

∴∠OBA＝60°，

∵折叠△AOB，

∴∠OBC＝∠ABC＝30°，

∴BC＝2OC，BO＝OC＝6，

∴OC＝2，

∴点C（2，0），

设直线BC解析式为：y＝kx+b，

解得：

∴直线BC解析式为：y＝﹣x+6；

（2）当点M与点B重合时，

由（1）可知：∠AMC＝∠MAC＝30°，

∴CM＝AC，

∴△ACM是等腰三角形，

∴当M为（0，6）时，△ACM是等腰三角形，

∵OC＝2，OA＝6，

∴AC＝4，

若AM＝AC＝4，

如图1：过点M作MH⊥AC，

∵∠MAH＝30°，

∴MH＝AM＝2，AH＝2MH＝6，

∴OH＝6﹣6或6+6，

∴点M（6﹣6，2）或（6+6，﹣2）

若AM＝MC，

如图2，过点M作MH⊥AC，

∵AM＝MC，MH⊥AC，

∴AH＝CH＝2，

∴OC＝4，

∵∠MAH＝30°，

∴AH＝MH，

∴MH＝2，

∴点M（4，2），

综上所述：点M（6﹣6，2）或（6+6，﹣2）或（4，2）或（0，6）．