题目内容
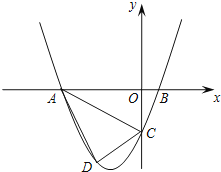
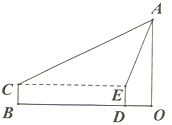
【题目】如图,在四边形ABCD中,AB∥DC,BC>AD,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).

(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)试探究:△BEF可以为等腰三角形吗?若能,求t的值;若不能,请说明理由.
【答案】(1)见解析;(2)DC=6.4cm;(3)当△EFB为等腰三角形时,t的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)根据三角形相似的判定定理即可得到结论;
(2)由△ACD∽△BAC,得![]() ,结合
,结合![]() =8cm,即可求解;
=8cm,即可求解;
(3)若△EFB为等腰三角形,可分如下三种情况:①当 BF=BE时, ②当EF=EB时,③当FB=FE时,分别求出t的值,即可.
(1)∵CD∥AB,
∴∠BAC=∠DCA,
又AC⊥BC,∠ACB=90°,
∴∠D=∠ACB=90°,
∴△ACD∽△BAC;
(2)在Rt△ABC中,![]() =8cm,
=8cm,
由(1)知,△ACD∽△BAC,
∴![]() ,
,
即: ![]() ,解得:DC=6.4cm;
,解得:DC=6.4cm;
(3)△BEF能为等腰三角形,理由如下:
由题意得:AF=2t,BE=t,
若△EFB为等腰三角形,可分如下三种情况:
①当 BF=BE时,10﹣2t=t,解得:t=![]() ;
;
②当EF=EB时,如图1,过点E作AB的垂线,垂足为G,
则![]() ,此时△BEG∽△BAC,
,此时△BEG∽△BAC,
∴![]() ,即
,即 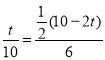 ,
,
解得:t=![]() ;
;
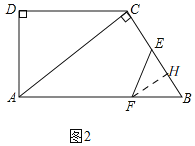
③当FB=FE时,如图2,过点F作AB的垂线,垂足为H,
则![]() ,此时△BFH∽△BAC,
,此时△BFH∽△BAC,
∴![]() ,即
,即 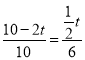 ,
,
解得:![]() ;
;
综上所述:当△EFB为等腰三角形时,t的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.


练习册系列答案
相关题目