题目内容
 如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移到△DCE,连接AD、BD,下列结论错误的是( )
如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移到△DCE,连接AD、BD,下列结论错误的是( )分析:由△ABC沿射线BC向右平移到△DCE,根据平移的性质:对应点的连线平行且相等得到AD与BC平行且相等,选项A正确,利用一组对边平行且相等的四边形为平行四边形得到ABCD为平行四边形,由三角形ABC为等边三角形可得出AB=BC,根据邻边相等的平行四边形为菱形可得出四边形ABCD为菱形,根据菱形的对角线互相垂直得到AC与BD垂直,再由平移的性质得到对应边平行,得到AC与DE平行,利用与平行线中的一条垂直,与另一条也垂直得到BD垂直于DE,选项B正确;同理可得出ACED为菱形,选项C正确;过A作AF垂直于BC,由三角形ABC为边长为2的等边三角形,根据三线合一得到BF为BC的一半,求出BF的长,在直角三角形ABF中,由AB及BF的长,利用勾股定理求出AF的长,然后利用底BC乘以高AF即可求出菱形ABCD的面积为2
,选项D错误,即可得出满足题意的选项.
| 3 |
解答:解:∵△ABC沿射线BC向右平移到△DCE,
∴AD=BC,AD∥BC,故选项A正确;
∴四边形ABCD为平行四边形,
又△ABC为等边三角形,∴AB=BC,
∴四边形ABCD为菱形,
∴AC⊥BD,
由平移可知:AC∥DE,
则DE⊥BD,故选项B正确;
∵△ABC沿射线BC向右平移到△DCE,
∴AD=CE,AD∥CE,
∴四边形ACED为平行四边形,
由平移可得△DCE也为等边三角形,
∴DE=CE,
∴四边形ACED为菱形,选项C正确;
过A作AF⊥BC,如图所示:

∵△ABC为边长为2的等边三角形,
∴BF=CF=
BC=1,
在Rt△ABF中,AB=2,BF=1,
根据勾股定理得:AF=
=
,
则S菱形ABCD=BC•AF=2
,选项D错误,
则原题结论错误的选项为D.
故选D
∴AD=BC,AD∥BC,故选项A正确;
∴四边形ABCD为平行四边形,
又△ABC为等边三角形,∴AB=BC,
∴四边形ABCD为菱形,
∴AC⊥BD,
由平移可知:AC∥DE,
则DE⊥BD,故选项B正确;
∵△ABC沿射线BC向右平移到△DCE,
∴AD=CE,AD∥CE,
∴四边形ACED为平行四边形,
由平移可得△DCE也为等边三角形,
∴DE=CE,
∴四边形ACED为菱形,选项C正确;
过A作AF⊥BC,如图所示:

∵△ABC为边长为2的等边三角形,
∴BF=CF=
| 1 |
| 2 |
在Rt△ABF中,AB=2,BF=1,
根据勾股定理得:AF=
| AB2-BF2 |
| 3 |
则S菱形ABCD=BC•AF=2
| 3 |
则原题结论错误的选项为D.
故选D
点评:此题考查了菱形的性质与判定,等边三角形的性质,以及平移的性质,灵活运用平移性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
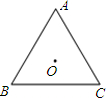 如图,△ABC是边长为a的等边三角形,O为△ABC的中心.将△ABC绕着中心O旋转120°.
如图,△ABC是边长为a的等边三角形,O为△ABC的中心.将△ABC绕着中心O旋转120°. 点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D. (2013•溧水县一模)如图,△ABC是边长为4的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连结BD,交AC于F.
(2013•溧水县一模)如图,△ABC是边长为4的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连结BD,交AC于F.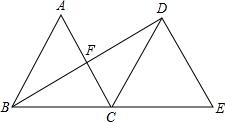 (2012•湘潭)如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F.
(2012•湘潭)如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F. 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点做一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为
如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点做一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为