题目内容
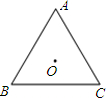 如图,△ABC是边长为a的等边三角形,O为△ABC的中心.将△ABC绕着中心O旋转120°.
如图,△ABC是边长为a的等边三角形,O为△ABC的中心.将△ABC绕着中心O旋转120°.①直接写出△ABC的内切圆半径r和外接圆半径R分别是多少?
②设点D、E、F分别在边AB、BC、CA上,且AD=2DB,BE=2EC,CF=2FA,试画出△DEF,说明它的形状,并计算它的周长;
③根据“线动成面”的道理,△ABC的三条边AB、BC和CA在旋转过程中扫过的部分组成的平面图形的形状是什么?并计算出此图形的面积.
分析:①O点到各定点的距离是外接圆半径R,O到各边的距离就是内接圆半径r;
②易知△DEF是等边三角形,可借助直角三角形求出其边长,继而得出其周长;
③△ABC旋转过程中扫过的部分组成的平面图形的形状是三角形的外接圆与内切圆所形成的圆环,大圆的面积减去小圆的面积即可求得.
②易知△DEF是等边三角形,可借助直角三角形求出其边长,继而得出其周长;
③△ABC旋转过程中扫过的部分组成的平面图形的形状是三角形的外接圆与内切圆所形成的圆环,大圆的面积减去小圆的面积即可求得.
解答:解:①内切圆半径r=
a,外接圆半径R=
a;
②如图画出△DEF,可知它是等边三角形.
取BE的中点M,连接DM,
由BD=BM=
a,且∠B=60°,得等边△BDM,
∴DM=ME=
a,∠MDE=∠MED,
又∠BMD=60°,
∴∠MED=
∠BMD=30°,
∴∠BDE=90°,
在Rt△BDE中,DE=
BD=
a,
∴等边△DEF的周长=
a;
③图形的形状是:三角形的外接圆与内切圆所形成的圆环.
∵圆环的大圆半径是△ABC外接圆半径R,小圆半径是△ABC内切圆半径r,
∴圆环的面积=πR2-πr2=π•
a2-π•
a2=
πa2.
| ||
| 6 |
| ||
| 3 |
②如图画出△DEF,可知它是等边三角形.
取BE的中点M,连接DM,
由BD=BM=
| 1 |
| 3 |
∴DM=ME=
| 1 |
| 3 |
又∠BMD=60°,
∴∠MED=
| 1 |
| 2 |
∴∠BDE=90°,
在Rt△BDE中,DE=
| 3 |
| ||
| 3 |
∴等边△DEF的周长=
| 3 |
③图形的形状是:三角形的外接圆与内切圆所形成的圆环.
∵圆环的大圆半径是△ABC外接圆半径R,小圆半径是△ABC内切圆半径r,
∴圆环的面积=πR2-πr2=π•
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 4 |
点评:本题考查了旋转的性质、三角形的内、外接圆及圆面积的计算,考查了知识点比较多,熟记其计算公式,是解答的关键,考查了学生的空间想象能力.

练习册系列答案
相关题目
 点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D. (2013•溧水县一模)如图,△ABC是边长为4的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连结BD,交AC于F.
(2013•溧水县一模)如图,△ABC是边长为4的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连结BD,交AC于F.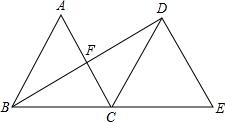 (2012•湘潭)如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F.
(2012•湘潭)如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F. 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点做一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为
如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点做一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为