题目内容
 (2013•溧水县一模)如图,△ABC是边长为4的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连结BD,交AC于F.
(2013•溧水县一模)如图,△ABC是边长为4的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连结BD,交AC于F.(1)猜想BD与DE的位置关系,并证明你的结论;
(2)求△BDE的面积S.
分析:(1)BD与DE垂直,理由为:由平移及等边三角形的性质得到BC=CD,∠BCD=120°,利用等腰三角形的性质及内角和定理求出∠CBD=30°,而∠E=60°,确定出∠BDE为直角,即可得证;
(2)由∠CBD为30°,得到BF为角平分线,利用三线合一得到BF垂直于AC,F为AC的中点,在直角三角形BCF中,由BC与CF长,利用勾股定理求出BF的长,继而确定出BD的长,由平移的性质得到DE=AC,即可求出三角形BDE的面积.
(2)由∠CBD为30°,得到BF为角平分线,利用三线合一得到BF垂直于AC,F为AC的中点,在直角三角形BCF中,由BC与CF长,利用勾股定理求出BF的长,继而确定出BD的长,由平移的性质得到DE=AC,即可求出三角形BDE的面积.
解答:解:(1)垂直,理由为:
由平移的性质得:AB=AC=BC=CE=CD=DE,∠E=∠DCE=∠ABC=60°,
∴∠DCB=120°,
又BC=CD,
∴∠CBD=∠CDB=30°,
∴∠BDE=90°,
∴BD⊥DE;
(2)∵∠CBD=30°,即BF为角平分线,AB=BC,
∴F为AC中点,即FC=2,BF⊥AC,
在Rt△BFC中,根据勾股定理得:BF=2
,
∵BC=CD,CF⊥BD,∴F为BD中点,
∴DB=2BF=4
,
则S△BDE=
•DB•DE=
×4
×4=8
.
由平移的性质得:AB=AC=BC=CE=CD=DE,∠E=∠DCE=∠ABC=60°,
∴∠DCB=120°,
又BC=CD,
∴∠CBD=∠CDB=30°,
∴∠BDE=90°,
∴BD⊥DE;
(2)∵∠CBD=30°,即BF为角平分线,AB=BC,
∴F为AC中点,即FC=2,BF⊥AC,
在Rt△BFC中,根据勾股定理得:BF=2
| 3 |
∵BC=CD,CF⊥BD,∴F为BD中点,
∴DB=2BF=4
| 3 |
则S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题考查了等边三角形的性质,勾股定理,以及平移性质,熟练掌握等边三角形的性质是解本题的关键.

练习册系列答案
相关题目
 (2013•溧水县一模)如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是
(2013•溧水县一模)如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是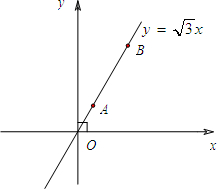 (2013•溧水县一模)如图,在平面直角坐标系中,A、B为正比例函数
(2013•溧水县一模)如图,在平面直角坐标系中,A、B为正比例函数