Question

【题目】我们已经知道，形如的无理数的化简要借助平方差公式：

例如：。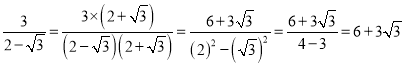

下面我们来看看完全平方公式在无理数化简中的作用。

问题提出：该如何化简？

建立模型：形如的化简，只要我们找到两个数，使，这样，，那么便有：，

问题解决：化简，

解：首先把化为，这里，，由于4+3=7，，

即（，，

∴

模型应用1：

利用上述解决问题的方法化简下列各式：

（1）；（2）；

模型应用2：

（3）在中，，，，那么边的长为多少？（结果化成最简）。

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）按照题目做法，令，即可求出结果；

（2）先将化为，再按照（1）的做法计算即可.

（3）利用勾股定理算出BC再化简即可.

（1）这里，由于，

即，

所以；

（2）首先把化为，这里，，由于，，

即，，

所以

（3）在中，由勾股定理得，

所以，

所以，