Question

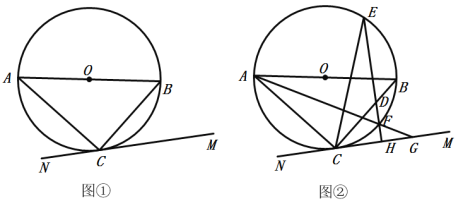
【题目】如图，公路MN为东西走向，在点M北偏东36.5°方向上，距离5千米处是学校A；在点M北偏东45°方向上距离千米处是学校B．（参考数据：，）．

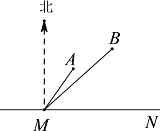
（1）求学校A，B两点之间的距离

（2）要在公路MN旁修建一个体育馆C，使得A，B两所学校到体育馆C的距离之和最短，求这个最短距离．

Answer 1

【答案】（1）km;（2）km.

【解析】

（1）过点A作CD//MN，BE⊥MN，在Rt△ACM中求出CM，AC，在Rt△MBE中求出BE，ME，继而得出AD，BD的长度，在Rt△ABD中利用勾股定理可得出AB的长度．

（2）作点B关于MN的对称点G，连接AG交MN于点P，点P即为站点，求出AG的长度即可．

（1）过点A作CD//MN，BE⊥MN，如图：

在Rt△ACM中，∠CMA＝36.5°，AM＝5km，

∵sin36.5°＝＝0.6，

∴CA＝3，MC＝4km，

在Rt△MBE中，∠NMB＝45°，MB＝km，

∵sin45°＝＝，

∴BE＝6，ME＝6km，

∴AD＝CDCA＝MECA＝3km，BD＝BEDE＝BECM＝2km，

在Rt△ABD中，AB＝km．

（2）作点B关于MN的对称点G，连接AG交MN于点P，连接PB，点P即为站点，

此时PA＋PB＝PA＋PG＝AG，即A，B两所学校到体育馆C的距离之和最短为AG长

在Rt△ADG中，AD=3，DG=DE+EG=DE+BE=4+6=10，∠ADG=90°，

∴AG＝＝km．

答：最短距离为km．