题目内容
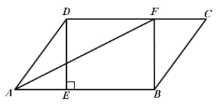
【题目】已知,如图 1,六边形 ABCDEF 的每一个内角都相等.
(1)六边形 ABCDEF 每一个内角的度数是 ;
(2)在图 1 中,若 AF 2 ,AB 4 ,BC 3 ,CD 1 ,则 DE ,EF ;
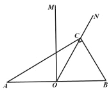
(3)如图 2,在(2)的条件下,若 M 、N 分别为边 AF 、 AB 的中点,连接 CM 、DN交于点 G ,求![]() 的值.
的值.
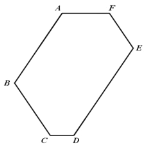
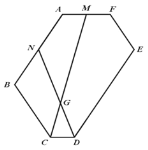
图 1 图 2
【答案】(1) 120°;(2) 5,2 ;(3)![]() .
.
【解析】
(1)用六边形的内角和除以6可得每个内角度数;(2)延长AE,BC,DE,得到一个等边三角形,根据等边三角形性质可求得DE和EF;(3)延长FA、DN交与点P,延长AB、DC交与点Q,证△BQC为等边三角形,求出AN=BN=2,QN=5,QD=4,再证AF∥QD
得![]() ,求出AP,再由AM=1得MP=AP+AM=
,求出AP,再由AM=1得MP=AP+AM=![]() ,所以
,所以![]() .
.
解:(1)120°;
(2)5,2;
(3)延长FA、DN交与点P,延长AB、DC交与点Q,
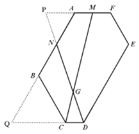
∵∠ABC=∠BCD= 120°,
∴∠QBC=∠QCB= 60°,
∴∠BQC=60°,即△BQC为等边三角形,
∵N为AB的中点,AB=4,
∴AN=BN=2,
∴QN=5,
∵QD=QC+CD,
∴QD=4,
∵∠BAF= 120°,
∴∠BQC+∠BAF= 180°,
∴AF∥QD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵M为AF的中点,
∴AM=1,
∴MP=AP+AM=![]()
∴![]() ,
,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目