题目内容
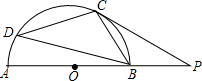如图，AB为半⊙O的直径，延长AB到P，使BP=| 1 |
| 2 |
| A、20° | B、25° |
| C、30° | D、40° |
分析：连接OC；由BP=
AB，可得BP与⊙O的半径相等，即OP=2OC，由此可求得∠P=30°，∠COP=60°，进而由圆周角定理求得∠BDC的度数．
| 1 |
| 2 |
解答：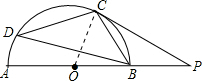
解：连接OC，则∠OCP=90°；
∵BP=
AB，
∴OB=BP=OC，即OP=2OC，
∴∠OPC=30°，∠POC=60°，
∴∠BDC=
∠POC=30°，
故选C．
解：连接OC，则∠OCP=90°；∵BP=
| 1 |
| 2 |
∴OB=BP=OC，即OP=2OC，
∴∠OPC=30°，∠POC=60°，
∴∠BDC=
| 1 |
| 2 |
故选C．
点评：此题主要考查了切线的性质、直角三角形的性质以及圆周角定理的综合应用，难度不大．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
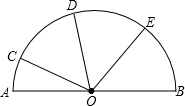
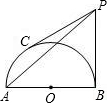如图，AB为半⊙O的直径，C为半圆弧的三等分点，过B，C两点的半⊙O的切线交于点P，若AB的长是2a，则PA的长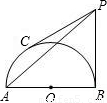是
AB，PC切半⊙O于点C，点D是弧AC上和点C不重合的一点，则∠BDC的度数是（ ）