题目内容
已知:如图,AB为半⊙O的直径,C、D、E为半圆弧上的点, |
| CD |
 |
| DE |
 |
| EB |

分析:利用在同圆中等弧所对的圆心角相等可得∠COD、∠DOE、∠BOE都为55°,则∠AOC可解.
解答:解:∵
=
=
,∠BOE=55°,
∴∠COD=∠DOE=∠BOE=55°,
∴∠AOC=180°-∠COD-∠DOE-∠BOE=15°.
 |
| CD |
 |
| DE |
 |
| EA |
∴∠COD=∠DOE=∠BOE=55°,
∴∠AOC=180°-∠COD-∠DOE-∠BOE=15°.
点评:本题利用了在同圆中等弧所对的圆心角相等和平角的概念求解.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
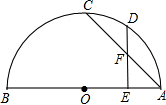 已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①
已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.① =
= =
= ,∠BOE=55°,则∠AOC的度数为________度.
,∠BOE=55°,则∠AOC的度数为________度.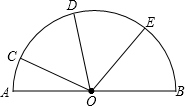
 =
= =
= ,∠BOE=55°,则∠AOC的度数为 度.
,∠BOE=55°,则∠AOC的度数为 度.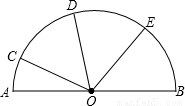
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.