题目内容
【题目】如图,△ABC中,∠ACB=90°,BC=6,AB=10.点Q与点B在AC的同侧,且AQ⊥AC.
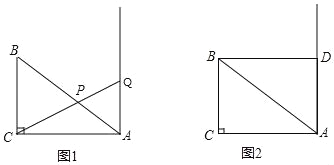
(1)如图1,点Q不与点A重合,连结CQ交AB于点P.设AQ=x,AP=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(2)是否存在点Q,使△PAQ与△ABC相似,若存在,求AQ的长;若不存在,请说明理由;
(3)如图2,过点B作BD⊥AQ,垂足为D.将以点Q为圆心,QD为半径的圆记为⊙Q.若点C到⊙Q上点的距离的最小值为8,求⊙Q的半径.
【答案】(1)![]() ;(2)在点Q,使△ABC∽△QAP,此时AQ=
;(2)在点Q,使△ABC∽△QAP,此时AQ=![]() ;(3)⊙Q的半径为9或
;(3)⊙Q的半径为9或![]() .
.
【解析】
试题分析:(1)先由平行线分线段成比例得出,![]() 代值即可得出结论;
代值即可得出结论;
(2)先判断出要使△PAQ与△ABC相似,只有∠QPA=90°,进而由相似得出比例式即可得出结论;
(3)分点C在⊙O内部和外部两种情况,用勾股定理建立方程求解即可.
试题解析:(1)∵AQ⊥AC,∠ACB=90°,∴AQ∥BC,∴![]() ,∵BC=6,AC=8,∴AB=10,
,∵BC=6,AC=8,∴AB=10,
∵AQ=x,AP=y,∴![]() ,∴
,∴![]() ;
;
(2)∵∠ACB=90°,而∠PAQ与∠PQA都是锐角,∴要使△PAQ与△ABC相似,只有∠QPA=90°,
即CQ⊥AB,此时△ABC∽△QAC,则![]() ,∴AQ=
,∴AQ=![]() .故存在点Q,使△ABC∽△QAP,此时AQ=
.故存在点Q,使△ABC∽△QAP,此时AQ=![]() ;
;
(3)∵点C必在⊙Q外部,∴此时点C到⊙Q上点的距离的最小值为CQ﹣DQ.
设AQ=x.①当点Q在线段AD上时,QD=6﹣x,QC=6﹣x+8=14﹣x,
∴x2+82=(14﹣x)2,解得:x=![]() ,即⊙Q的半径为
,即⊙Q的半径为![]() .
.
②当点Q在线段AD延长线上时,QD=x﹣6,QC=x﹣6+8=x+2,
∴x2+82=(x+2)2,解得:x=15,即⊙Q的半径为9.
∴⊙Q的半径为9或![]() .
.

【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1