题目内容
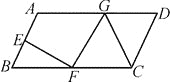
【题目】【问题情境】如图①,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小丽给出的提示是:如图②,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
请根据小丽的提示进行证明.




【变式探究】如图③,当点P在BC延长线上时,其余条件不变,试猜想PD、PE、CF三者之间的数量关系并证明.
【结论运用】如图④,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值.
【答案】见解析;CF=PD+PE ;PG+PH的值为4.
【解析】【问题情境】
分析:【问题情境】连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
【变式探究】连接AP,由△ABP与△ACP面积之差等于△ABC的面积可以证得:CF=PD-PE.
【结论运用】先证BE=BF,过点E作EQ⊥BF,垂足为Q,利用问题情境中的结论可得PG+PH=EQ,易证EQ=DC,故只需求出DC即可.
详解:证明:连接AP,如图②,
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP+S△ACP,
∴![]() ABCF=
ABCF=![]() ABPD+
ABPD+![]() ACPE.
ACPE.
∵AB=AC,
∴CF=PD+PE.
【变式探究】
证明:连接AP,如图③.
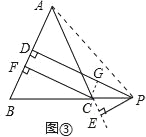
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP﹣S△ACP,
∴![]() ABCF=
ABCF=![]() ABPD﹣
ABPD﹣![]() ACPE.
ACPE.
∵AB=AC,
∴CF=PD﹣PE.
【结论运用】
过点E作EQ⊥BC,垂足为Q,如图④,
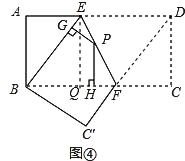
∵四边形ABCD是矩形,
∴AD=BC,∠C=∠ADC=90°.
∵AD=8,CF=3,
∴BF=BC﹣CF=AD﹣CF=5.
由折叠可得:DF=BF,∠BEF=∠DEF.
∴DF=5.
∵∠C=90°,
∴DC=![]() =4.
=4.
∵EQ⊥BC,∠C=∠ADC=90°,
∴∠EQC=90°=∠C=∠ADC,
∴四边形EQCD是矩形,
∴EQ=DC=4.
∵AD∥BC,
∴∠DEF=∠EFB.
∵∠BEF=∠DEF,
∴∠BEF=∠EFB,
∴BE=BF.
由问题情境中的结论可得:PG+PH=EQ,
∴PG+PH=4,
∴PG+PH的值为4.

【题目】列方程解应用题:
为参加学校运动会,七年级一班和七年级二班准备购买运动服. 下面是某服装厂给出的运动服价格表:
购买服装数(套) | 1~35 | 36~60 | 61及61以上 |
每套服装价(元) | 60 | 50 | 40 |
已知两班共有学生67人(每班学生人数都不超过60人),如果两班单独购买服装,每人只买一套,那么一共应付3650元. 问七年级一班和七年级二班各有学生多少人?