题目内容
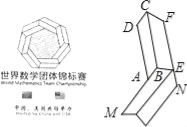
【题目】第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行，其会徽如图所示，它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形．设AD=a，AB=b，CF=c，EF=d，则该会徽内外两个正七边形的周长之和为（ ）
A．7（a+b+c﹣d） B．7（a+b﹣c+d）
C．7（a﹣b+c+d） D．7（b+c+d﹣a）
【答案】C
【解析】
试题分析：根据全等形的性质得到BM=AD，EN=CF，然后根据正七边形的周长公式计算即可．
如图，∵它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形， ∴AM=BM﹣AB=AD﹣AB=a﹣b，FN=EF+EN=EF+CF=c+d，
∴内外两个正七边形的周长之和为7（a﹣b）+7（c+d）=7（a﹣b+c+d），
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
