题目内容
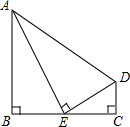 如图,∠ABC=∠DCB=90°,AB=BC,点E是BC的中点,EA⊥ED.
如图,∠ABC=∠DCB=90°,AB=BC,点E是BC的中点,EA⊥ED.求证:(1)△ABE∽△ECD;
(2)∠EAD=∠EAB.
分析:(1)由已知得∠BAE+∠BEA=90°,∠DEC+∠BEA=90°,等量代换得∠BAE=∠DEC,再由∠ABE=∠ECD=90°证得△ABE∽△ECD;
(2)由AB=BC,点E是BC的中点,CE=BE=
AB,再由△ABE∽△ECD推出
=
,已知EA⊥ED推出∠DEA=90°=∠ABC,所以△AED∽△ABE,从而得出∠EAD=∠EAB.
(2)由AB=BC,点E是BC的中点,CE=BE=
| 1 |
| 2 |
| DE |
| AE |
| BE |
| AB |
解答:证明:(1)∵∠BAE+∠BEA=90°
∠DEC+∠BEA=90°(2分)
∴∠BAE=∠DEC(1分)
又∵∠ABE=∠ECD=90°
∴△ABE∽△ECD(1分)
(2)∵点E是BC的中点
∴CE=BE=
BC(1分)
∵AB=BC∴CE=BE=
AB(1分)
∵△ABE∽△ECD
∴
=
=
(1分)
∵
=
∴
=
(1分)
∵EA⊥ED
∴∠DEA=90°=∠ABC
∴△AED∽△ABE(1分)
∴∠EAD=∠EAB(1分)
∠DEC+∠BEA=90°(2分)
∴∠BAE=∠DEC(1分)
又∵∠ABE=∠ECD=90°
∴△ABE∽△ECD(1分)
(2)∵点E是BC的中点
∴CE=BE=
| 1 |
| 2 |
∵AB=BC∴CE=BE=
| 1 |
| 2 |
∵△ABE∽△ECD
∴
| DE |
| AE |
| CE |
| AB |
| 1 |
| 2 |
∵
| BE |
| AB |
| 1 |
| 2 |
∴
| DE |
| AE |
| BE |
| AB |
∵EA⊥ED
∴∠DEA=90°=∠ABC
∴△AED∽△ABE(1分)
∴∠EAD=∠EAB(1分)
点评:此题考查的知识点是相似三角形的判定与性质,关键是由已知证明角相等推出三角形相似;通过已知推出三角形相似得出角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
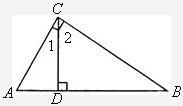
 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
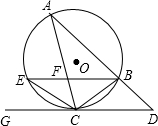 ,且CB=CE.
,且CB=CE.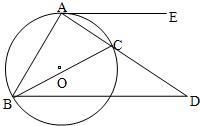 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.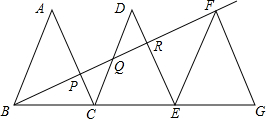 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且