题目内容
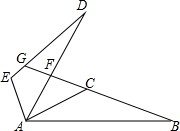
①如图1,在矩形ABCD中,E、F为BC上两点,且BE=CF,求证:∠BAF=∠CDE;
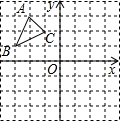
②如图2,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将△AOB绕原点顺时针方向旋转90°后记作△A′OB′;
①画出旋转后的图形并写出A′、B′的坐标;
②求在旋转过程中线段OA扫过的面积.
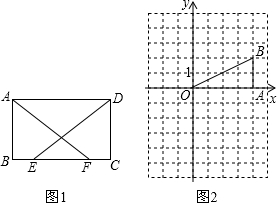
②如图2,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将△AOB绕原点顺时针方向旋转90°后记作△A′OB′;
①画出旋转后的图形并写出A′、B′的坐标;
②求在旋转过程中线段OA扫过的面积.

①证明:在矩形ABCD中,AB=CD,∠B=∠C=90°,
∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE,
在△ABF和△DCE中,
∵
,
∴△ABF≌△DCE(SAS),
∴∠BAF=∠CDE;
②(1)∵点B(4,2),
∴tan∠BOA=
=
;
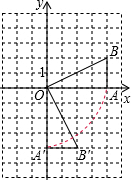
(2)①如图,△A′OB′即为所求作的图形;
点A′(0,-4),B′(2,-4);
②线段OA扫过的面积=
=4π.
∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE,
在△ABF和△DCE中,
∵
|
∴△ABF≌△DCE(SAS),
∴∠BAF=∠CDE;
②(1)∵点B(4,2),
∴tan∠BOA=
| 2 |
| 4 |
| 1 |
| 2 |
(2)①如图,△A′OB′即为所求作的图形;
点A′(0,-4),B′(2,-4);
②线段OA扫过的面积=
| 90•π•42 |
| 360 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目