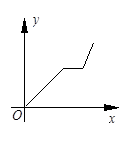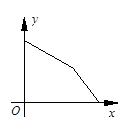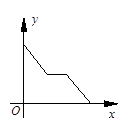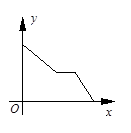题目内容
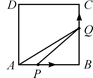
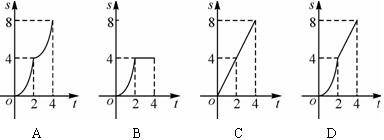
如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿点A→B方向运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿B→C→D方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是( )


D
试题分析:本题应分两段进行解答,①点P在AB上运动,点Q在BC上运动,②点P在AB上运动,点Q在CD上运动,依次得出S与t的关系式即可得出函数图象.
①点P在AB上运动,点Q在BC上运动,此时AP=t,QB=2t,
故可得S= AP•QB=t2,函数图象为抛物线;
AP•QB=t2,函数图象为抛物线;
②点P在AB上运动,点Q在CD上运动,
此时AP=t,△APQ底边AP上的高维持不变,为正方形的边长4,
故可得S= AP×4=2t,函数图象为一次函数.
AP×4=2t,函数图象为一次函数.
综上可得总过程的函数图象,先是抛物线,然后是一次增函数.
故选D.
本题涉及了动点问题的函数图象,解答本题关键是分段求解,注意在第二段时,△APQ底边AP上的高维持不变,难度一般.
①点P在AB上运动,点Q在BC上运动,此时AP=t,QB=2t,
故可得S=
 AP•QB=t2,函数图象为抛物线;
AP•QB=t2,函数图象为抛物线;②点P在AB上运动,点Q在CD上运动,
此时AP=t,△APQ底边AP上的高维持不变,为正方形的边长4,
故可得S=
 AP×4=2t,函数图象为一次函数.
AP×4=2t,函数图象为一次函数.综上可得总过程的函数图象,先是抛物线,然后是一次增函数.
故选D.
本题涉及了动点问题的函数图象,解答本题关键是分段求解,注意在第二段时,△APQ底边AP上的高维持不变,难度一般.

练习册系列答案
相关题目
 在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3.直线AB与x轴交于点C,则△AOC的面积为( )
在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3.直线AB与x轴交于点C,则△AOC的面积为( )
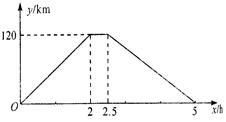
 与注水时间
与注水时间 的函数图象大致为( )
的函数图象大致为( )

 满足不等式组
满足不等式组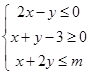 ,且
,且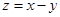 的最小值为
的最小值为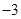 ,则实数
,则实数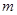 的值是 .
的值是 . =x+1的解x0满足1<x0<2,则k可能是( )
=x+1的解x0满足1<x0<2,则k可能是( ) ,0),B(2,0),若点C在一次函数
,0),B(2,0),若点C在一次函数 的图象上,且△ABC为直角三角形,则满足条件的点C有 ( )
的图象上,且△ABC为直角三角形,则满足条件的点C有 ( )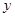 (千米)与时间
(千米)与时间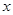 (小时)的函数关系的大致图象是( )
(小时)的函数关系的大致图象是( )