题目内容
正方形ABCD中，AB=1，分别以A、C为圆心作两个半径为R、r（R＞r）的圆，当R、r满足什么条件时，⊙A与⊙C有2个交点
- A.R+r＞
- B.R-r＜＜R+r
- C.R-r＞
- D.0＜R-r＜
B
分析：由题可知，圆心距是正方形的对角线的长为，又因为两圆相交，所以R-r＜＜R+r．
解答：∵圆心距是正方形的对角线的长为，
⊙A与⊙C有2个交点，
∴两圆相交．
∴R-r＜＜R+r．
故选B．
点评：本题利用了两圆相交时，圆心距介于两圆半径的差与和之间的性质求解．
分析：由题可知，圆心距是正方形的对角线的长为
，又因为两圆相交，所以R-r＜＜R+r．解答：∵圆心距是正方形的对角线的长为
，⊙A与⊙C有2个交点，
∴两圆相交．
∴R-r＜
＜R+r．故选B．
点评：本题利用了两圆相交时，圆心距介于两圆半径的差与和之间的性质求解．
练习册系列答案
相关题目
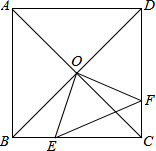（2013•临沂）如图，正方形ABCD中，AB=8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动，设运动时间为t（s），△OEF的面积为s（cm2），则s（cm2）与t（s）的函数关系可用图象表示为（ ）
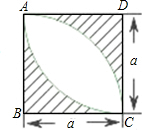如图，在正方形ABCD中，画2个半径为a的四分之一圆，用代数式表示阴影部分的面积为
如图，在正方形ABCD中，AB=4，E在BC边上，BE=1，F是AC上一动点，则EF+BF的最小值是