题目内容
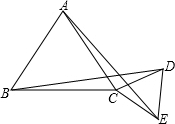 如图,已知△ABC和△CDE都是等边三角形,问:线段AE、BD的长度有什么关系?请说明理由.
如图,已知△ABC和△CDE都是等边三角形,问:线段AE、BD的长度有什么关系?请说明理由.
解:AE=BD.
∵△ABC是等边三角形,(已知)
∴AC=BC,∠ACB=60°.(等边三角形性质)
∵△CDE是等边三角形,(已知)
∴CD=CE,∠DCE=60°.(等边三角形性质)
∴∠ACB=∠DCE.(等量代换)
∴∠ACB+∠ACD=∠DCE+∠ACD.(等式性质)
即∠BCD=∠ACE.
在△ACE和△BCD中,
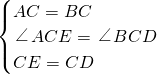 ,
,
∴△ACE≌△BCD.(SAS)
∴AE=BD.(全等三角形对应边相等)
分析:由△ABC和△CDE都是等边三角形,易得AB=BC,CD=CE,∠ACB=∠DCE=60°,即可得∠BCD=∠ACE,根据SAS即可证得△ACE≌△BCD,则可得AE=BD.
点评:此题考查了全等三角形的判定与性质与等边三角形的性质.此题难度不大,注意数形结合思想的应用是解此题的关键.
∵△ABC是等边三角形,(已知)
∴AC=BC,∠ACB=60°.(等边三角形性质)
∵△CDE是等边三角形,(已知)
∴CD=CE,∠DCE=60°.(等边三角形性质)
∴∠ACB=∠DCE.(等量代换)
∴∠ACB+∠ACD=∠DCE+∠ACD.(等式性质)
即∠BCD=∠ACE.
在△ACE和△BCD中,
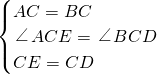 ,
,∴△ACE≌△BCD.(SAS)
∴AE=BD.(全等三角形对应边相等)
分析:由△ABC和△CDE都是等边三角形,易得AB=BC,CD=CE,∠ACB=∠DCE=60°,即可得∠BCD=∠ACE,根据SAS即可证得△ACE≌△BCD,则可得AE=BD.
点评:此题考查了全等三角形的判定与性质与等边三角形的性质.此题难度不大,注意数形结合思想的应用是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目

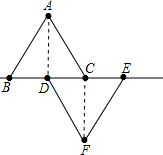 ,连接AD、CF.
,连接AD、CF. 19、如图,已知△ABC和△A″B″C″及点O.
19、如图,已知△ABC和△A″B″C″及点O. 23、如图,已知△ABC和两条相交于O点且夹角为60°的直线m、n.
23、如图,已知△ABC和两条相交于O点且夹角为60°的直线m、n.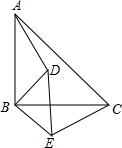 (2012•南岗区二模)如图,已知△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,求证:AD=CE.
(2012•南岗区二模)如图,已知△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,求证:AD=CE.