题目内容
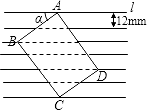
【题目】如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED′=30°,则∠BFC′的度数为_________。

【答案】30°.
【解析】
根据平角的定义计算出∠DED′=150°,再根据折叠的性质得∠DEF=∠D′EF,所以∠DEF=![]() ∠DED′=75°.再由平行线的性质可得∠DEF=∠EFB=75°,∠DEF+∠EFC=180°,即可得∠EFC=105°,由折叠的性质可得∠EFC=∠EF C′=105°,由此可得∠BFC′=∠EF C′-∠EFB=105°-75°30°.
∠DED′=75°.再由平行线的性质可得∠DEF=∠EFB=75°,∠DEF+∠EFC=180°,即可得∠EFC=105°,由折叠的性质可得∠EFC=∠EF C′=105°,由此可得∠BFC′=∠EF C′-∠EFB=105°-75°30°.
∵∠AED′=30°,
∴∠DED′=180°-∠AED′=180°-30°=150°,
∵长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,
∴∠DEF=∠D′EF,
∴∠DEF=![]() ∠DED′=
∠DED′=![]() ×150°=75°.
×150°=75°.
∵AD∥BC,
∴∠DEF=∠EFB=75°,∠DEF+∠EFC=180°,
∴∠EFC=105°,
∵长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,
∴∠EFC=∠EF C′=105°,
∴∠BFC′=∠EF C′-∠EFB=105°-75°30°.
故答案为:30°.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目