��Ŀ����
��ͼ���ı���ABCD�����Σ��Խ���AC��BD���ڵ�O����AC=80��BD=60������M��N�ֱ���ÿ��1����λ���ٶȴӵ�A��Dͬʱ�������ֱ���A��O��D��D��A�˶�������N�����Aʱ��M��Nͬʱֹͣ�˶������˶�ʱ��Ϊt�룮
��1��������ABCD���ܳ���
��2���ǡ�DMN�����ΪS����S����t�Ľ���ʽ������S�����ֵ��
��3����t=30��ʱ�����߶�OD�Ĵ�ֱƽ�������Ƿ���ڵ�P��ʹ�á�DPO=��DON�������ڣ������ĵ�P�м������������P���߶�OD�ľ��룻�������ڣ���˵�����ɣ�
�⣺��1��������ABCD�У�
��AC��BD��AC=80��BD=60���� ��
��
������ABCD���ܳ�Ϊ200��
��2������M��MP��AD��������P��
�ٵ�0��t��40ʱ�����ͼ1��
�� ��
��
��MP=AM•sin��OAD= t��
t��
S= DN•MP=
DN•MP= ��t��
��t�� t=
t= t2��
t2��
�ڵ�40��t��50ʱ�����ͼ2��MD=70��t��
�� ��
��
��MP= ��70��t����
��70��t����
��S��DMN= DN•MP=
DN•MP= ��t��
��t�� ��70��t��=
��70��t��= t2+28t=
t2+28t= ��t��35��2+490��
��t��35��2+490��
��S����t�Ľ���ʽΪ ��
��
��0��t��40ʱ��S��t�����������t=40ʱ�����ֵΪ480��
��40��t��50ʱ��S��t���������С�����ֵ������480��
����������S�����ֵΪ480��
��3������2����P��ʹ�á�DPO=��DON��
���ͼ3��ʾ������N��NF��OD�ڵ�F��
��NF=ND•sin��ODA=30�� =24��
=24��
DF=ND•cos��ODA=30�� =18��
=18��
��OF=12���� ��
��
����NOD��ƽ���߽�NF�ڵ�G������G��GH��ON�ڵ�H��
��FG=GH��
��S��ONF= OF•NF=S��OGF+S��OGN=
OF•NF=S��OGF+S��OGN= OF•FG+
OF•FG+ ON•GH=
ON•GH= ��OF+ON��•FG��
��OF+ON��•FG��
�� ��
��
�� ��
��
��OD�д�����OD�Ľ���ΪK���ɶԳ��Կ�֪����DPK= ��DPO=
��DPO= ��DON=��FOG��
��DON=��FOG��
�� ��
��
��PK= ��
��
�������εĶԳ��Կ�֪�����߶�OD���·��������P����OD��ԳƵĵ�P�䡣
�����������P��OD�ľ��붼��
���������������1�����ݹ��ɶ��������ε����ʣ�������ε��ܳ���
��2���ڶ���M��N�˶������У��ٵ�0��t��40ʱ�����ͼ1��ʾ���ڵ�40��t��50ʱ�����ͼ2��ʾ���ֱ����S�Ĺ�ϵʽ��Ȼ�����ö��κ���������������ֵ��
��3�����ͼ3��ʾ����Rt��PKD�У�DK�����������ֻ�����tan��DPK���ɣ�Ϊ�ˣ��ڡ�ODM�У��������ߣ�����Rt��OND������NODƽ����OG�����GOF=��DPK����Rt��OGF�У����tan��GOF��ֵ���Ӷ���������
���⣺��ͼ4��ʾ����ON�Ĵ�ֱƽ���ߣ���OD�Ĵ�ֱƽ����EF�ڵ�I�����ӽ�OI��IN������N��NG��OD��NH��EF������ֱ�ΪG��H��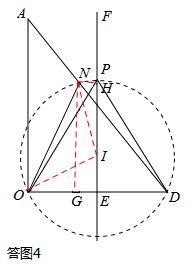
��t=30ʱ��DN=OD=30����֪��DNG�ס�DAO��
�� ����
���� ��
��
��NG=24��DG=18��
��EF��ֱƽ��OD����OE=ED=15��EG=NH=3��
��OI=R��EI=x����
��Rt��OEI����R2=152+x2 ��
��Rt��NIH����R2=32+��24��x��2 ��
�ɢ١��ڿɵã� ��
��
��PE=PI+IE= ��
��
���ݶԳ��Կɵã���BD�·�������һ����P��Ҳ����������
�����������P����OD�ľ��붼�� ��
��

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�





 ����C��1��
����C��1��