题目内容
 如图,已知C是线段AB的中点,D是BC的中点,E是AD的中点,F是AE的中点,那么线段AF是线段AC的
如图,已知C是线段AB的中点,D是BC的中点,E是AD的中点,F是AE的中点,那么线段AF是线段AC的
- A.

- B.

- C.

- D.
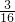
C
分析:设CD=a,首先根据D是BC的中点,得出BC=2a.由C是线段AB的中点,得出AC=BC=2a,进而求出AD=3a,再由E是AD的中点,得出AE=1.5a.由F是AE的中点,得出AF=0.75a.从而AF、AC都用含a的代数式表达,最后算出它们的比值,得出结果.
解答:∵D是BC的中点,
∴CD=BD.
设CD=a,则BD=a,BC=2a.
∵C是线段AB的中点,
∴AC=BC=2a,
∴AD=AC+CD=3a.
又∵E是AD的中点,
∴AE= AD=1.5a.
AD=1.5a.
∵F是AE的中点,
∴AF= AE=0.75a.
AE=0.75a.
∴AF:AC=0.75a:2a=3:8.
故选C.
点评:利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.本题中设CD=a之后,利用中点性质及线段的和、差将线段AF、AC都用含a的代数式表达出来,是解决本题的关键.
分析:设CD=a,首先根据D是BC的中点,得出BC=2a.由C是线段AB的中点,得出AC=BC=2a,进而求出AD=3a,再由E是AD的中点,得出AE=1.5a.由F是AE的中点,得出AF=0.75a.从而AF、AC都用含a的代数式表达,最后算出它们的比值,得出结果.
解答:∵D是BC的中点,
∴CD=BD.
设CD=a,则BD=a,BC=2a.
∵C是线段AB的中点,
∴AC=BC=2a,
∴AD=AC+CD=3a.
又∵E是AD的中点,
∴AE=
 AD=1.5a.
AD=1.5a.∵F是AE的中点,
∴AF=
 AE=0.75a.
AE=0.75a.∴AF:AC=0.75a:2a=3:8.
故选C.
点评:利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.本题中设CD=a之后,利用中点性质及线段的和、差将线段AF、AC都用含a的代数式表达出来,是解决本题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
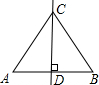 如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )
如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )| A、AE=BE | B、AD=BD | C、AB=AC | D、ED=AD |
如图,已知C是线段AB的中点,则CD等于( )


| A、AD-BD | ||
B、
| ||
C、
| ||
D、AD-
|
 如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE.
如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE. (2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1
(2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1