题目内容
已知一个三角形的周长和面积分别是84、210,一个单位圆在它的内部沿着三边匀速无摩擦地滚动一周后回到原来的位置(如图),则这个三角形的内部以及边界没有被单位圆滚过的部分的面积是______(结果保留准确值).


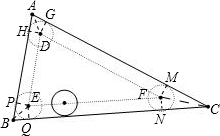
如图;
设△ABC的内切圆半径为R,△DEF的内切圆半径为r;
依题意有:
×84×R=210,即R=5;
易知:△DEF∽△ABC,且r:R=4:5,
∴C△DEF=
C△ABC=67.2;
易知:被圆滚过的三角形内部的三角形也和△ABC相似;
且其内切圆半径为:R-2=3,即其面积=(
)2S△ABC=75.6;
由图知:S四边形AHDG=2S△AGD=AG•1=AG,同理S四边形PEQB=BQ,S四边形CNFM=CM;
∴S四边形AHDG+S四边形PEQB+S四边形CNFM=AG+CM+BQ=
(C△ABC-C△DEF)=8.4;
而S扇形DHG+S扇形PEQ+S扇形FMN=S单位圆=π,
∴所求的面积=75.6+8.4-π=84-π.
设△ABC的内切圆半径为R,△DEF的内切圆半径为r;
依题意有:
| 1 |
| 2 |
易知:△DEF∽△ABC,且r:R=4:5,
∴C△DEF=
| 4 |
| 5 |
易知:被圆滚过的三角形内部的三角形也和△ABC相似;
且其内切圆半径为:R-2=3,即其面积=(
| 3 |
| 5 |
由图知:S四边形AHDG=2S△AGD=AG•1=AG,同理S四边形PEQB=BQ,S四边形CNFM=CM;
∴S四边形AHDG+S四边形PEQB+S四边形CNFM=AG+CM+BQ=
| 1 |
| 2 |
而S扇形DHG+S扇形PEQ+S扇形FMN=S单位圆=π,
∴所求的面积=75.6+8.4-π=84-π.


练习册系列答案
相关题目