题目内容
 如图,AB、CD相交于点E,现给出如下三个论断:①∠A=∠C;②AD=CB;③AE=CE.请你选择其中两个论断为条件,另外一个论断为结论,构造一个命题.在构成的所有命题中,真命题有
如图,AB、CD相交于点E,现给出如下三个论断:①∠A=∠C;②AD=CB;③AE=CE.请你选择其中两个论断为条件,另外一个论断为结论,构造一个命题.在构成的所有命题中,真命题有2
2
个.分析:在△ADE和△CBE中,②③无法证明全等.因为SSA无法证明三角形全等.而其他两个能证明另外一个.本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.
解答:解:由分析可知②③无法证明①,而其他两个能证明另外一个,
所以真命题有2个.
故填:2;
附:①选择的真命题是:①②得③;
证明:在△ADE和△CBE中,
∵∠A=∠C,∠AED=∠CEB,AD=CB,
∴△ADE≌△CBE.
∴AE=CE.
②选择命题二:①③得②;
证明:在△ADE和△CBE中,
∵∠A=∠C,AE=CE,∠AED=∠CEB,
∴△ADE≌△CBE.
∴AD=CB.
所以真命题有2个.
故填:2;
附:①选择的真命题是:①②得③;
证明:在△ADE和△CBE中,
∵∠A=∠C,∠AED=∠CEB,AD=CB,
∴△ADE≌△CBE.
∴AE=CE.
②选择命题二:①③得②;
证明:在△ADE和△CBE中,
∵∠A=∠C,AE=CE,∠AED=∠CEB,
∴△ADE≌△CBE.
∴AD=CB.
点评:本题考查了全等三角形的判定及性质;题目比较简单,直接根据全等三角形的判定方法容易找到正确的结论.

练习册系列答案
相关题目
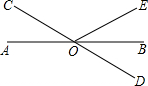 如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是
如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是 如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是
如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是 如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC=
如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC= (2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
(2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点. 已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.
已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.