��Ŀ����
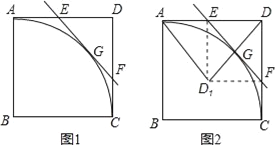
����Ŀ����ͼ1��ʾ����������ABCD�У�AB=1�� ![]() ���Ե�BΪԲ�ģ�AB��Ϊ�뾶��Բ��һ�λ�����E�DZ�AD�ϵĶ��㣨��E���A��D���غϣ�����E��
���Ե�BΪԲ�ģ�AB��Ϊ�뾶��Բ��һ�λ�����E�DZ�AD�ϵĶ��㣨��E���A��D���غϣ�����E��![]() ����Բ�����ߣ�����DC�ڵ�F��GΪ�е㣮
����Բ�����ߣ�����DC�ڵ�F��GΪ�е㣮
��1����֤��EA=EG��
��2����AE=x��FC=y����y����x�ĺ�����ϵʽ����ֱ��д��x��ȡֵ��Χ��
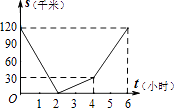
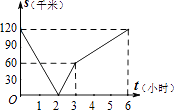
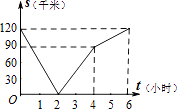
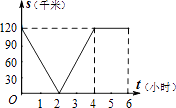
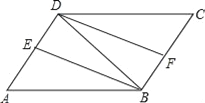
��3����ͼ2��ʾ������DEF��ֱ��EF���ۺ�á�D1EF������AD1��D1D����̽��������E�˶����δ�ʱ����AD1D���ED1F���ƣ���˵�����ɣ�
���𰸡���1��֤������������2��y=![]() ��0��x��1������3������E�˶���AD���е�ʱ����AD1D���ED1F���ƣ����ɼ�������
��0��x��1������3������E�˶���AD���е�ʱ����AD1D���ED1F���ƣ����ɼ�������
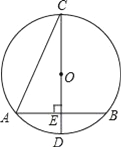
�������������������1��֤��AD��ԲB�����ߣ������߳��������ɵó����ۣ�
��2���������߳������������ε����ʵõ��йص��߶���x��y��ʾ���ٸ��ݹ��ɶ�������������ϵʽ��
��3���������߳������ҵ���֮��Ĺ�ϵ���Ӷ����������Σ����������ε����ʵõ������Ƕ�Ӧ��ȣ��Ӷ�֤�����������ƣ�
�����������1�����ı���ABCD�������Σ����BAD=��D=90�㣬AD=CD=AB=1����AD��BA����AD��ԲB�����ߣ���EG��ԲB�����ߣ���EA=EG��
��2����EF��ԲB�ڵ�G����EA=EG��FC=FG��
��AE=x��FC=y��EF=x+y��DE=1��x��DF=1��y��
��Rt��DEF�У����ݹ��ɶ������ã���x+y��2=��1��x��2+��1��y��2
��y=![]() ��0��x��1����
��0��x��1����
��3������E�˶���AD���е�ʱ����AD1D���ED1F���ƣ��������£�
��ֱ��EF���߶�DD1�ڵ�H�������⣬�ã���EDF�ա�ED1F��EF��DD1��DH=D1H��
��AE=![]() ��AD=1����AE=ED����EH��AD1����AD1D=��EHD=90�㣮
��AD=1����AE=ED����EH��AD1����AD1D=��EHD=90�㣮
�֡ߡ�ED1F=��EDF=90�㣬���FD1D=��AD1D����D1F��AD�����ADD1=��DD1F=��EFD=45�㣬
���ED1F�ס�AD1D��