ЬтФПФкШн
ЁОЬтФПЁПжмФЉаЁУїКЭЭЌбЇУЧШЅЁАТЬВЉдАЁБЕФЗуКўзјДЌЃЌЙлЩЭЗчОАЃЛШчЭМЃЌаЁУїе§дкAДІЕФаЁДЌЩЯЃЌBДІаЁДЌЩЯЕФгЮПЭЗЂЯжЕуAдкЕуBЕФе§ЮїЗНЯђЩЯЃЌCДІаЁДЌЩЯЕФгЮПЭЗЂЯжЕуAдкЕуCЕФФЯЦЋЖЋ30ЁуЗНЯђЩЯЃЌвбжЊЕуCдкЕуBЕФББЦЋЮї60ЁуЗНЯђЩЯЃЌЧвBЁЂCСНЕиЯрОр120УзЃЎ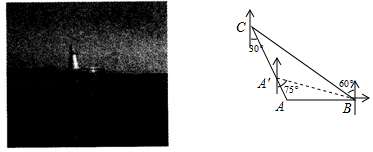
ЃЈ1ЃЉЧѓГіДЫЪБЕуAЕНЕуCЕФОрРыЃЛ
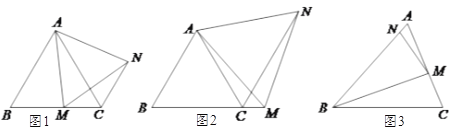
ЃЈ2ЃЉШєаЁУїДгAДІбиACЗНЯђЯђCЪЛШЅЃЌЕБЕНДяЕуAЁфЪБЃЌВтЕУЕуBдкAЁфЕФФЯЦЋЖЋ75ЁуЕФЗНЯђЩЯЃЌЧѓДЫЪБаЁУїЫљГЫзјЕФаЁДЌзпЕФОрРыЃЎЃЈзЂЃКНсЙћБЃСєИљКХЃЉ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКзїCDЁЭBAНЛBAЕФбгГЄЯпгкЕуDЃЌ
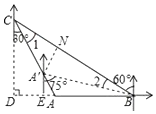
гЩЬтвтПЩЕУЃЌBC=120УзЃЌЁЯCBD=30ЁуЃЌ
дђCD=60УзЃЌ
ЁпЁЯDCA=30ЁуЃЌ
ЁрAC= ![]() УзЃЌ
УзЃЌ
МДДЫЪБЕуAЕНЕуCЕФОрРыЪЧ40 ![]() УзЃЛ
УзЃЛ
ЃЈ2ЃЉ
НтЃКзїAЁфNЁЭBCгкЕуNЃЌзїAЁфEЁЭBAНЛBAЕФбгГЄЯпгкЕуEЃЌ

гЩЬтвтПЩЕУЃЌ
ЁЯ1=30ЁуЃЌЁЯEAЁфB=Ёф75ЁуЃЌЁЯEAЁфA=30ЁуЃЌЁЯCBD=30ЁуЃЌ
дђЁЯAAЁфB=45ЁуЃЌ
ЁрЁЯ2=15ЁуЃЌ
ЁрЁЯAЁфBE=15ЁуЃЌ
ЁрAЁфN=AЁфEЃЌ
ЩшAAЁф=xЃЌ
дђAЁфE= ![]() ЃЌ
ЃЌ
ЁрAЁфN= ![]() ЃЌ
ЃЌ
ЁрCAЁф= ![]() ЃЌ
ЃЌ
ЁпCA= ![]() ЃЌ
ЃЌ
Ёрx+ ![]() x=40
x=40 ![]() ЃЌ
ЃЌ
ЕУx= ![]()
Д№ЃКДЫЪБаЁУїЫљГЫзјЕФаЁДЌзпЕФОрРыЪЧЃЈ ![]() ЃЉУзЃЎ
ЃЉУзЃЎ
ЁОНтЮіЁПЃЈ1ЃЉИљОнЬтвтзїГіКЯЪЪЕФИЈжњЯпЃЌШЛКѓИљОнШёНЧШ§НЧКЏЪ§МДПЩЧѓЕУACЕФГЄЃЛЃЈ2ЃЉИљОнЬтвтКЭШёНЧШ§НЧКЏЪ§ПЩвдЧѓЕУаЁУїЫљГЫзјЕФаЁДЌзпЕФОрРыЃЎ
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫЙигкЗНЯђНЧЮЪЬтЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮежИББЛђжИФЯЗНЯђЯпгыФПБъЗНЯђ ЯпЫљГЩЕФаЁгк90ЁуЕФЫЎЦННЧЃЌНазіЗНЯђНЧВХФме§ШЗНтД№ДЫЬтЃЎ

 аЁЬьВХПЮЪБзївЕЯЕСаД№АИ
аЁЬьВХПЮЪБзївЕЯЕСаД№АИ вЛПЮЫФСЗЯЕСаД№АИ
вЛПЮЫФСЗЯЕСаД№АИ ЛЦИдаЁзДдЊТњЗжГхДЬЮЂВтбщЯЕСаД№АИ
ЛЦИдаЁзДдЊТњЗжГхДЬЮЂВтбщЯЕСаД№АИ аТИЈНЬЕМбЇЯЕСаД№АИ
аТИЈНЬЕМбЇЯЕСаД№АИ бєЙтЭЌбЇвЛЯпУћЪІШЋгХКУОэЯЕСаД№АИ
бєЙтЭЌбЇвЛЯпУћЪІШЋгХКУОэЯЕСаД№АИ