题目内容
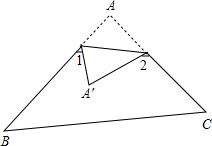 已知△ABC中,∠A=50°,将∠A向三角形内折叠,如图所示,那么∠1+∠2=
已知△ABC中,∠A=50°,将∠A向三角形内折叠,如图所示,那么∠1+∠2=
- A.130°
- B.50°
- C.100°
- D.150°
C
分析:先根据平角定义,可得∠1=180°-2∠3,∠2=180°-2∠4,再利用等式性质可得∠1+∠2=360°-2(∠3+∠4),而∠3+∠4可用180-∠A来代替,进而可求∠1+∠2.
解答: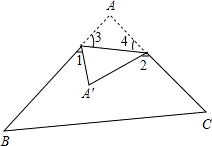 解:如右图所示,
解:如右图所示,
∵∠1=180°-2∠3,
∠2=180°-2∠4,
∴∠1+∠2=360°-2(∠3+∠4)=360°-2×(180°-∠A)
=2∠A=100°.
故选C.
点评:本题考查了三角形内角和定理、翻折变换,解题的关键是知道翻折前后的图形全等.
分析:先根据平角定义,可得∠1=180°-2∠3,∠2=180°-2∠4,再利用等式性质可得∠1+∠2=360°-2(∠3+∠4),而∠3+∠4可用180-∠A来代替,进而可求∠1+∠2.
解答:
 解:如右图所示,
解:如右图所示,∵∠1=180°-2∠3,
∠2=180°-2∠4,
∴∠1+∠2=360°-2(∠3+∠4)=360°-2×(180°-∠A)
=2∠A=100°.
故选C.
点评:本题考查了三角形内角和定理、翻折变换,解题的关键是知道翻折前后的图形全等.

练习册系列答案
相关题目
 情况;若不可能,请说明理由.
情况;若不可能,请说明理由.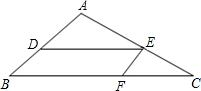 已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为
已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为 如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F 如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )
如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )