题目内容
【题目】如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是______.
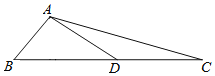
【答案】15
【解析】
延长AD到点E,使DE=AD=6,连接CE,可证明△ABD≌△CED,所以CE=AB,再利用勾股定理的逆定理证明△CDE是直角三角形,即△ABD为直角三角形,进而可求出△ABD的面积.
解:延长AD到点E,使DE=AD=6,连接CE,
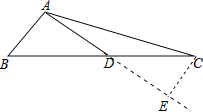
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△CED中,
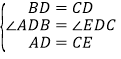 ,
,
∴△ABD≌△CED(SAS),
∴CE=AB=5,∠BAD=∠E,
∵AE=2AD=12,CE=5,AC=13,
∴CE2+AE2=AC2,
∴∠E=90°,
∴∠BAD=90°,
即△ABD为直角三角形,
∴△ABD的面积=![]() ADAB=15.
ADAB=15.
故答案为:15.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】已知![]() 两点在数轴上从各自位置同时向左右匀速运动(规定向右为正)
两点在数轴上从各自位置同时向左右匀速运动(规定向右为正)
时间 位置 | 0秒 | 3秒 | 6秒 |
| 6 | -3 | |
| 2 | 8 |
(1)请你将上面表格补充完整;
(2)点![]() 、点
、点![]() 运动过程中是否会相遇,如果能相遇,请求出相遇的时间
运动过程中是否会相遇,如果能相遇,请求出相遇的时间
(3)点![]() 、点
、点![]() 两点间的距离能否为5个单位长度?若能,请求出它们运动的时间
两点间的距离能否为5个单位长度?若能,请求出它们运动的时间