题目内容
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,以
的中点,以![]() 为一边向外作等边三角形
为一边向外作等边三角形![]() ,连结
,连结![]() .
.
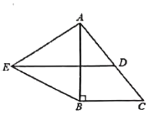
(1)证明: ![]() ;
;
(2)探索![]() 与
与![]() 满足怎样的数量关系时,四边形
满足怎样的数量关系时,四边形![]() 是平行四边形;
是平行四边形;
【答案】(1)见解析;(2)当![]() 或
或![]() 时,四边形
时,四边形![]() 是平行四边形,见解析.
是平行四边形,见解析.
【解析】
(1)连结BD,根据直角三角形的性质可得BD=![]() AC=AD,利用等边三角形的性质可得AE=BE,然后证明△ADE≌△BDE,进而可求出∠AED=∠BED=30°,
AC=AD,利用等边三角形的性质可得AE=BE,然后证明△ADE≌△BDE,进而可求出∠AED=∠BED=30°,
然后再证明∠BED+∠EBC=180°,从而可得结论;
(2)当AB=![]() AC或AC=2AB时,四边形DCBE是平行四边形,首先利用三角函数求出∠C=30°,然后证明DC∥BE,再有DE∥BC,可得四边形DCBE是平行四边形.
AC或AC=2AB时,四边形DCBE是平行四边形,首先利用三角函数求出∠C=30°,然后证明DC∥BE,再有DE∥BC,可得四边形DCBE是平行四边形.
解:(1)连结![]() .
.
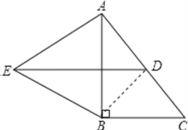
因为点![]() 为
为![]() 的斜边
的斜边![]() 的中点,
的中点,
所以![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() ,
,
在![]() 与
与![]() 中,
中,
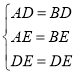 ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(2)当![]() 或
或![]() 时,四边形
时,四边形![]() 是平行四边形.
是平行四边形.
理由:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,∴四边形
,∴四边形![]() 是平行四边形.
是平行四边形.
故答案为:(1)见解析;(2)当![]() 或
或![]() 时,四边形
时,四边形![]() 是平行四边形,见解析.
是平行四边形,见解析.

练习册系列答案
相关题目
【题目】课题小组从某市2000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果制成了如下的统计表.
等级 | 人数 | 百分比 |
优秀 | 200 | 20% |
良好 | 600 | 60% |
及格 | 150 | 15% |
不及格 | 50 |
|
(1)![]() 的值为______;
的值为______;
(2)请从表格中任意选取一列数据,绘制合理的统计图来表示;(绘制一种即可)
(3)估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.