题目内容
如图甲,在平面直角坐标系中,直线 分别交x轴、y轴点A、B,⊙O的半径为
分别交x轴、y轴点A、B,⊙O的半径为 个单位长度.点P为直线
个单位长度.点P为直线 上的动点,过点P作⊙O的切线PC、PD ,切点分别为C、D,且PC⊥PD.
上的动点,过点P作⊙O的切线PC、PD ,切点分别为C、D,且PC⊥PD.

(1)写出点A、B的坐标:A ( ),B ( );
(2)试说明四边形OCPD的形状(要有证明过程);
(3)求点P的坐标;
(4)如图乙 ,若直线 将⊙O的圆周分成两段弧长之比为1∶3,请直接写出b的值:b= .
将⊙O的圆周分成两段弧长之比为1∶3,请直接写出b的值:b= .
 分别交x轴、y轴点A、B,⊙O的半径为
分别交x轴、y轴点A、B,⊙O的半径为 个单位长度.点P为直线
个单位长度.点P为直线 上的动点,过点P作⊙O的切线PC、PD ,切点分别为C、D,且PC⊥PD.
上的动点,过点P作⊙O的切线PC、PD ,切点分别为C、D,且PC⊥PD.
(1)写出点A、B的坐标:A ( ),B ( );
(2)试说明四边形OCPD的形状(要有证明过程);
(3)求点P的坐标;
(4)如图乙 ,若直线
 将⊙O的圆周分成两段弧长之比为1∶3,请直接写出b的值:b= .
将⊙O的圆周分成两段弧长之比为1∶3,请直接写出b的值:b= .
(1)A(4,0),B(0,4);(2)正方形;(3)(1,3)或(3,1);(4) 或-
或-
 或-
或-
试题分析:(1)分别求得直线
 与x轴、y轴的交点坐标即可得到结果;
与x轴、y轴的交点坐标即可得到结果;(2)连接OC、OD,根据切线的性质可得∠PCO=∠PDO=90°,再有PC⊥PD可得四边形OCPD为矩形,再结合OC=OD即可证得结论;
(3)根据P在直线y=-x+4上,可设P(m,-m+4),根据勾股定理即可求得结果;
(4)分两种情形,直线
 将圆周分成两段弧长之比为1∶3,可知被割得的弦所对的圆心角为90
将圆周分成两段弧长之比为1∶3,可知被割得的弦所对的圆心角为90 ,又直线
,又直线 与坐标轴的夹角为45
与坐标轴的夹角为45 ,即可求得结果.
,即可求得结果.(1)在
 中,当x=0时,y=4,当y=0时,x=4
中,当x=0时,y=4,当y=0时,x=4则A(4,0),B(0,4);
(2)连接OC、OD

∵PC、PD为⊙O的切线
∴∠PCO=∠PDO=90°
∵PC⊥PD
∴四边形OCPD为矩形
∵OC=OD
∴四边形OCPD是正方形;
(3)∵P在直线y=-x+4上,
∴设P(m,-m+4),则OF=m,PF=-m+4,
∵∠PFO=90°,
∴OF2+PF2=PO2,
∴ m2+ (-m+4)2=(
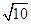 )2,
)2,解得m=1或3,
∴P的坐标为(1,3)或(3,1)

(4)分两种情形,直线
 将圆周分成两段弧长之比为1∶3,可知被割得的弦所对的圆心角为90
将圆周分成两段弧长之比为1∶3,可知被割得的弦所对的圆心角为90 ,又直线
,又直线 与坐标轴的夹角为45
与坐标轴的夹角为45 ,如图可知,分两种情况,所以,b的值为
,如图可知,分两种情况,所以,b的值为 或-
或- .
. 
点评:本题知识点较多,综合性强,难度较大,需要学生熟练掌握一次函数的性质的应用.

练习册系列答案
相关题目
 经过点A(0,5),B(1,4).
经过点A(0,5),B(1,4).
 与直线AB相交于点C,求点C的坐标;
与直线AB相交于点C,求点C的坐标; 轴相交于点
轴相交于点 ,与反比例函数图象相交于点
,与反比例函数图象相交于点 ,
, 的面积为6.求一次函数和反比例函数的解析式.
的面积为6.求一次函数和反比例函数的解析式.

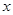 吨,请写出将粮食运往A、B两库的总运费
吨,请写出将粮食运往A、B两库的总运费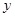 (元)与
(元)与 ,点
,点 是一次函数
是一次函数 图象上的两个点,且
图象上的两个点,且 ,那么
,那么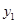
 (填“>”或“<”)
(填“>”或“<”)
