ΧβΡΩΡΎ»ί
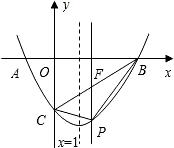 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψAΓΔCΒΡΉχ±ξΖ÷±πΈΣΘ®-1Θ§0Θ©ΓΔΘ®0Θ§-
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψAΓΔCΒΡΉχ±ξΖ÷±πΈΣΘ®-1Θ§0Θ©ΓΔΘ®0Θ§-| 3 |
Θ®1Θ©«σΗΟΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©»τ…ηΒψPΒΡΚαΉχ±ξΈΣmΘ§”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈPFΒΡ≥ΛΘΜ
Θ®3Θ©«σΓςPBCΟφΜΐΒΡΉν¥σ÷ΒΘ§≤Δ«σ¥Υ ±ΒψPΒΡΉχ±ξΘ°
Ζ÷ΈωΘΚ¥ΥΧβΈΡΉ÷±»ΫœΕύΘ§Εχ«“ΆΦœσ“≤±»ΫœΗ¥‘”Θ§Υυ“‘ΫβΧβ ±–η“ΣάμΫβΧβ“βΘ°
Θ®1Θ©Ω…“‘≤…”Ο¥ΐΕ®œΒ ΐΖ®«σΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘ§“ρΈΣΒψAΘ®-1Θ§0Θ©ΓΔCΘ®0Θ§-
Θ©‘ΎΚ· ΐΆΦœσ…œΘ§Ε‘≥Τ÷αΈΣx=1Θ§“≤Ω…«σΒΟAΒΡΕ‘≥ΤΒψBΒΡΉχ±ξΈΣΘ®3Θ§0Θ©Θ§Ν–ΖΫ≥ΧΉιΦ¥Ω…«σΒΟΫβΈω ΫΘΜ
Θ®2Θ©œ»«σΒΟ÷±œΏBCΒΡΫβΈω ΫΈΣy=
x-
Θ§‘ρΩ…«σΒΟΒψFΒΡΉχ±ξΈΣ(mΘ§
m-
)Θ§‘Ό«σΒΟΒψPΒΡΉίΉχ±ξΈΣ
m2-
m-
Θ§Ω…ΒΟœΏΕΈPFΒΡ≥ΛΘΜ
Θ®3Θ©άϊ”ΟΟφΜΐΚΆΘ§ΓςPBCΒΡΟφΜΐS=SΓςCPF+SΓςBPF=
PF•BOΦ¥Ω…«σΒΟΘ°
Θ®1Θ©Ω…“‘≤…”Ο¥ΐΕ®œΒ ΐΖ®«σΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘ§“ρΈΣΒψAΘ®-1Θ§0Θ©ΓΔCΘ®0Θ§-
| 3 |
Θ®2Θ©œ»«σΒΟ÷±œΏBCΒΡΫβΈω ΫΈΣy=
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| 3 |
Θ®3Θ©άϊ”ΟΟφΜΐΚΆΘ§ΓςPBCΒΡΟφΜΐS=SΓςCPF+SΓςBPF=
| 1 |
| 2 |
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©…ηΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΈΣy=ax2+bx+cΘ®aΓΌ0Θ§aΓΔbΓΔcΈΣ≥Θ ΐΘ©Θ§
”…≈ΉΈοœΏΒΡΕ‘≥Τ–‘÷ΣBΒψΉχ±ξΈΣΘ®3Θ§0Θ©Θ§
“άΧβ“βΒΟΘΚ
Θ§Θ®1Ζ÷Θ©
ΫβΒΟΘΚ
Θ§Θ®2Ζ÷Θ©
ΓύΥυ«σΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΈΣy=
x2-
x-
ΘΜΘ®3Ζ÷Θ©
Θ®2Θ©ΓΏPΒψΒΡΚαΉχ±ξΈΣmΘ§
ΓύPΒψΒΡΉίΉχ±ξΈΣ
m2-
m-
Θ§Θ®4Ζ÷Θ©
…η÷±œΏBCΒΡΫβΈω ΫΈΣy=kx+bΘ®kΓΌ0Θ§kΓΔb «≥Θ ΐΘ©Θ§
“άΧβ“βΘ§ΒΟ
Θ§
Γύ
Θ§
Ι ÷±œΏBCΒΡΫβΈω ΫΈΣy=
x-
Θ§Θ®5Ζ÷Θ©
ΓύΒψFΒΡΉχ±ξΈΣ(mΘ§
m-
)Θ§
ΓύPF=-
m2+
m(0ΘΦmΘΦ3)ΘΜΘ®6Ζ÷Θ©
Θ®3Θ©ΓΏΓςPBCΒΡΟφΜΐS=SΓςCPF+SΓςBPF=
PF•BO=
ΓΝ(-
m2+
m)ΓΝ3=-
(m-
)2+
Θ§
ΓύΒ±m=
±Θ§ΓςPBCΒΡΉν¥σΟφΜΐΈΣ
Θ§Θ®8Ζ÷Θ©
Α―m=
¥ζ»κy=
m2-
m-
Θ§
ΒΟy=-
Θ§
ΓύΒψPΒΡΉχ±ξΈΣ(
Θ§-
)Θ°Θ®10Ζ÷Θ©
”…≈ΉΈοœΏΒΡΕ‘≥Τ–‘÷ΣBΒψΉχ±ξΈΣΘ®3Θ§0Θ©Θ§
“άΧβ“βΒΟΘΚ
|
ΫβΒΟΘΚ
|
ΓύΥυ«σΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΈΣy=
| ||
| 3 |
2
| ||
| 3 |
| 3 |
Θ®2Θ©ΓΏPΒψΒΡΚαΉχ±ξΈΣmΘ§
ΓύPΒψΒΡΉίΉχ±ξΈΣ
| ||
| 3 |
2
| ||
| 3 |
| 3 |
…η÷±œΏBCΒΡΫβΈω ΫΈΣy=kx+bΘ®kΓΌ0Θ§kΓΔb «≥Θ ΐΘ©Θ§
“άΧβ“βΘ§ΒΟ
|
Γύ
|
Ι ÷±œΏBCΒΡΫβΈω ΫΈΣy=
| ||
| 3 |
| 3 |
ΓύΒψFΒΡΉχ±ξΈΣ(mΘ§
| ||
| 3 |
| 3 |
ΓύPF=-
| ||
| 3 |
| 3 |
Θ®3Θ©ΓΏΓςPBCΒΡΟφΜΐS=SΓςCPF+SΓςBPF=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
9
| ||
| 8 |
ΓύΒ±m=
| 3 |
| 2 |
9
| ||
| 8 |
Α―m=
| 3 |
| 2 |
| ||
| 3 |
2
| ||
| 3 |
| 3 |
ΒΟy=-
5
| ||
| 4 |
ΓύΒψPΒΡΉχ±ξΈΣ(
| 3 |
| 2 |
5
| ||
| 4 |
ΒψΤάΘΚ¥ΥΧβΩΦ≤ιΝΥ―ß…ζΒΡΉέΚœ”Π”ΟΡήΝΠΘ§“ΣΉΔ“β ΐ–ΈΫαΚœΘ§»œ’φΖ÷ΈωΘ§Ή–œΗ ΕΆΦΘ°ΉΔ“β¥ΐΕ®œΒ ΐΖ®«σΚ· ΐΒΡΫβΈω ΫΘ§ΉΔ“βΚ· ΐΫΜΒψΉχ±ξΒΡ«σΖ®Θ§ΉΔ“β»ΐΫ«–ΈΟφΜΐΒΡ«σΖ®Θ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξ÷–Θ§ΥΡ±Ώ–ΈOABC «Β»―ϋΧί–ΈΘ§CBΓΈOAΘ§OA=7Θ§AB=4Θ§ΓœCOA=60ΓψΘ§ΒψPΈΣx÷α…œΒΡ“ΜΗωΕ·ΒψΘ§ΒΪ «ΒψP≤Μ”κΒψ0ΓΔΒψA÷ΊΚœΘ°Ν§Ϋ”CPΘ§DΒψ «œΏΕΈAB…œ“ΜΒψΘ§Ν§Ϋ”PDΘ°
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξ÷–Θ§ΥΡ±Ώ–ΈOABC «Β»―ϋΧί–ΈΘ§CBΓΈOAΘ§OA=7Θ§AB=4Θ§ΓœCOA=60ΓψΘ§ΒψPΈΣx÷α…œΒΡ“ΜΗωΕ·ΒψΘ§ΒΪ «ΒψP≤Μ”κΒψ0ΓΔΒψA÷ΊΚœΘ°Ν§Ϋ”CPΘ§DΒψ «œΏΕΈAB…œ“ΜΒψΘ§Ν§Ϋ”PDΘ° Θ®2012•”ε±±«χ“ΜΡΘΘ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξxoy÷–Θ§“‘Ήχ±ξ‘≠ΒψOΈΣ‘≤–ΡΘ§3ΈΣΑκΨΕΜ≠‘≤Θ§¥”¥Υ‘≤ΡΎΘ®Αϋά®±ΏΫγΘ©ΒΡΥυ”–’ϊ ΐΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΘ©÷–»Έ“β―ûÓΜΗωΒψΘ§ΤδΚαΓΔΉίΉχ±ξ÷°ΚΆΈΣ0ΒΡΗ≈¬ «
Θ®2012•”ε±±«χ“ΜΡΘΘ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξxoy÷–Θ§“‘Ήχ±ξ‘≠ΒψOΈΣ‘≤–ΡΘ§3ΈΣΑκΨΕΜ≠‘≤Θ§¥”¥Υ‘≤ΡΎΘ®Αϋά®±ΏΫγΘ©ΒΡΥυ”–’ϊ ΐΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΘ©÷–»Έ“β―ûÓΜΗωΒψΘ§ΤδΚαΓΔΉίΉχ±ξ÷°ΚΆΈΣ0ΒΡΗ≈¬ « »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξ÷–Θ§Β»―ϋΧί–ΈABCDΒΡœ¬ΒΉ‘Ύx÷α…œΘ§«“BΒψΉχ±ξΈΣΘ®4Θ§0Θ©Θ§DΒψΉχ±ξΈΣΘ®0Θ§3Θ©Θ§‘ρAC≥ΛΈΣ
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξ÷–Θ§Β»―ϋΧί–ΈABCDΒΡœ¬ΒΉ‘Ύx÷α…œΘ§«“BΒψΉχ±ξΈΣΘ®4Θ§0Θ©Θ§DΒψΉχ±ξΈΣΘ®0Θ§3Θ©Θ§‘ρAC≥ΛΈΣ »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξxOy÷–Θ§“―÷ΣΒψAΘ®-5Θ§0Θ©Θ§P «Ζ¥±»άΐΚ· ΐ
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξxOy÷–Θ§“―÷ΣΒψAΘ®-5Θ§0Θ©Θ§P «Ζ¥±»άΐΚ· ΐ ΓœCOA=45ΓψΘ§Ε·ΒψP¥”ΒψO≥ωΖΔΘ§‘ΎΧί–ΈOABCΒΡ±Ώ…œ‘ΥΕ·Θ§¬ΖΨΕΈΣOΓζAΓζBΓζCΘ§ΒΫ¥οΒψC ±ΆΘ÷ΙΘ°Ής÷±œΏCPΘ°
ΓœCOA=45ΓψΘ§Ε·ΒψP¥”ΒψO≥ωΖΔΘ§‘ΎΧί–ΈOABCΒΡ±Ώ…œ‘ΥΕ·Θ§¬ΖΨΕΈΣOΓζAΓζBΓζCΘ§ΒΫ¥οΒψC ±ΆΘ÷ΙΘ°Ής÷±œΏCPΘ°